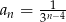/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 8627692

Dodaj do ulubionych
Dodaj do rozwiązanych

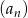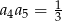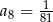Wyznacz wyraz ogólny ciągu geometrycznego (an) , w którym 1 a4a5 = 3 oraz a8 = 181 .

Rozwiązanie

Ze wzoru 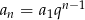n− 1 an = a1q na n -ty wyraz ciągu geometrycznego mamy układ równań

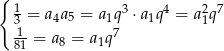
{ 13 = a4a5 = a1q3 ⋅a1q4 = a21q7 1-= a = a q7 81 8 1

Podstawiając 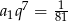7 -1 a1q = 81 z drugiego równania do pierwszego mamy

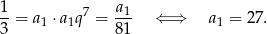
1 a1 --= a1 ⋅a1q7 = --- ⇐ ⇒ a1 = 27. 3 81

Zatem

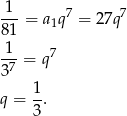
1 7 7 8-1 = a1q = 2 7q -1-= q7 3 7 1- q = 3.

Wyraz ogólny jest więc równy

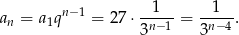
a = a qn− 1 = 27⋅ --1--= --1--. n 1 3n−1 3n− 4

 
Odpowiedź: an = -1n−4- 3

Wersja PDF