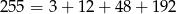/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 8899928

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.

Rozwiązanie

Szukamy rozkładu postaci

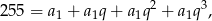
2 3 2 55 = a1 + a1q + a1q + a1q ,

gdzie

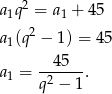
2 a1q = a1 + 4 5 a (q2 − 1) = 4 5 1 a = --45--. 1 q2 − 1

Podzieliliśmy powyżej przez 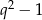q2 − 1 , ale łatwo sprawdzać, że 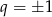q = ± 1 nie może spełniać warunków zadania.

Podstawiamy otrzymane wyrażenie do pierwszej równości i mamy

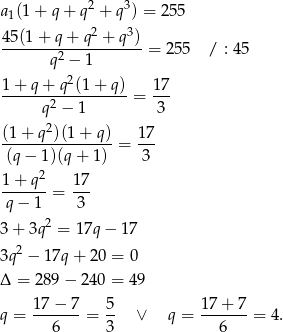
2 3 a1(1 + q+ q + q ) = 255 45(1-+-q-+-q2-+-q3)- q2 − 1 = 255 / : 45 1-+-q-+-q2(1-+-q) 17- q2 − 1 = 3 2 (1-+-q-)(1-+-q) = 17- (q− 1 )(q+ 1) 3 2 1-+-q--= 17- q− 1 3 2 3+ 3q = 17q − 1 7 3q2 − 17q + 20 = 0 Δ = 289 − 240 = 4 9 1-7−-7- 5- 17-+-7- q = 6 = 3 ∨ q = 6 = 4.

Jeżeli 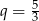q = 5 3 to

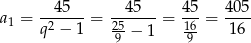
--45--- --45--- 45- 405- a1 = q2 − 1 = 25− 1 = 16 = 16 9 9

nie jest liczbą całkowitą.

Zatem 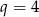q = 4 i mamy

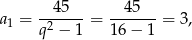
45 45 a1 = -2-----= -------= 3 , q − 1 16 − 1

co daje szukany rozkład

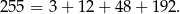
255 = 3 + 12 + 48 + 19 2.

 
Odpowiedź: 255 = 3+ 12+ 48 + 192

Wersja PDF