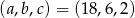/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 9342984

Dodaj do ulubionych
Dodaj do rozwiązanych

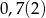Trzy liczby dodatnie a,b i c tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi 0,7(2) . Znajdź te liczby.

Rozwiązanie

Zamieńmy najpierw 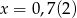x = 0,7(2) na ułamek zwykły.

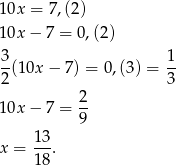
10x = 7,(2) 10x − 7 = 0,(2) 3 1 -(1 0x− 7) = 0,(3) = -- 2 3 10x − 7 = 2- 9 13 x = 18.

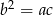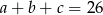Wiemy, że b2 = ac , a + b + c = 2 6 oraz

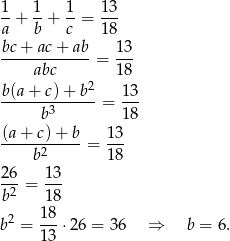
1- 1- 1- 13- a + b + c = 18 bc + ac + ab 13 -------------= --- abc 18 b-(a+-c)-+-b2 13- b3 = 18 (a + c) + b 13 ----------- = --- b2 18 2-6 1-3 b2 = 1 8 18 b2 = ---⋅26 = 36 ⇒ b = 6. 13

Skorzystaliśmy z faktu, że 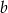b jest dodatnie. Mamy zatem

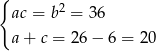
{ 2 ac = b = 3 6 a + c = 26 − 6 = 2 0

Można ten układ rozwiązać wprost, ale można też zauważyć, że na mocy wzorów Viète’a liczby a i c są pierwiastkami równania

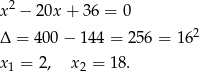
x2 − 20x + 36 = 0 Δ = 400 − 14 4 = 256 = 1 62 x1 = 2, x2 = 18 .

Mamy zatem dwa ciągi spełniające warunki zadania 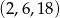(2,6 ,1 8) i (18,6,2) .  
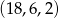Odpowiedź: 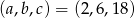(a,b,c) = (2 ,6,18) lub (a,b,c) = (1 8,6,2)

Wersja PDF