/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 9531461

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.

Rozwiązanie

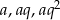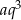Oznaczmy cztery początkowe wyrazy danego ciągu przez 2 a,aq,aq i 3 aq . Mamy zatem równania

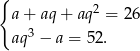
{ a + aq + aq2 = 26 aq3 − a = 52 .

Przekształćmy drugie równanie

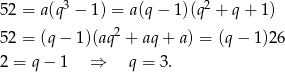
3 2 5 2 = a(q − 1) = a(q − 1)(q + q + 1) 5 2 = (q− 1)(aq2 + aq + a) = (q − 1)26 2 = q− 1 ⇒ q = 3.

Z drugiego równania mamy wtedy

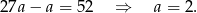
27a− a = 52 ⇒ a = 2.

Zatem piąty wyraz jest równy

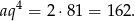
4 aq = 2 ⋅81 = 16 2.

 
Odpowiedź: 162

Wersja PDF