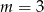/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 9573859

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań:

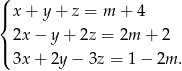
( |{ x + y + z = m + 4 2x − y+ 2z = 2m + 2 |( 3x + 2y− 3z = 1 − 2m .

Dla jakich wartości parametru 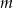m liczby 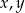x,y i z są kolejnymi wyrazami ciągu geometrycznego?

Rozwiązanie

Sposób rozwiązywania takich układów jest dość prosty – przy pomocy jednego równania pozbywamy się z dwóch pozostałych którejś niewiadomej i zostanie nam układ dwóch równań z dwoma niewiadomymi.

Odejmijmy od drugiego równania podwojone pierwsze i od trzeciego potrojone pierwsze (skracamy x ).

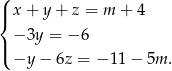
(| x + y + z = m + 4 { − 3y = − 6 |( −y − 6z = − 11 − 5m .

Z drugiego równania mamy 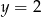y = 2 , a z trzeciego

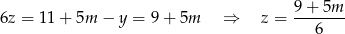
9 + 5m 6z = 11+ 5m − y = 9 + 5m ⇒ z = ------- 6

Z pierwszego równania mamy

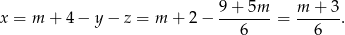
9-+-5m- m-+--3 x = m + 4 − y − z = m + 2 − 6 = 6 .

Liczby te tworzą ciąg geometryczny jeżeli 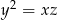y2 = xz , czyli

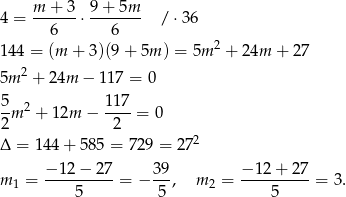
m + 3 9+ 5m 4 = ------⋅ ------- / ⋅36 6 6 2 14 4 = (m + 3)(9+ 5m ) = 5m + 2 4m + 27 2 5m + 24m − 117 = 0 5- 2 117- 2m + 1 2m − 2 = 0 2 Δ = 144 + 58 5 = 729 = 27 −-1-2−-2-7 39- −-12-+-27- m 1 = 5 = − 5 , m 2 = 5 = 3.

 
Odpowiedź: 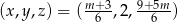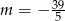(x,y ,z) = (m+-3,2, 9+5m-) 6 6 , 39 m = − 5 lub m = 3

Wersja PDF