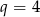/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 9896366

Dodaj do ulubionych
Dodaj do rozwiązanych

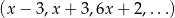Ciąg (x − 3,x+ 3,6x + 2,...) jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że 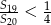SS19 < 14 20 , gdzie 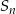Sn oznacza sumę n początkowych wyrazów tego ciągu.

Rozwiązanie

Trzy kolejne wyrazy 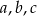a,b,c ciągu geometrycznego muszą spełniać warunek: 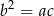b2 = ac . W naszej sytuacji prowadzi to do równania.

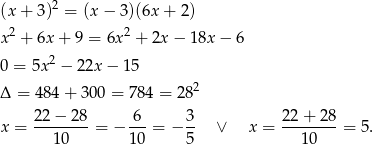
2 (x + 3 ) = (x− 3)(6x + 2) x 2 + 6x + 9 = 6x2 + 2x − 18x − 6 0 = 5x2 − 22x − 15 2 Δ = 48 4+ 3 00 = 784 = 28 22-−-28- -6- 3- 22-+-28- x = 10 = − 10 = − 5 ∨ x = 10 = 5.

W pierwszym przypadku 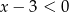x − 3 < 0 , więc musi być 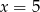x = 5 . Wtedy iloraz ciągu jest równy

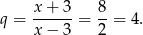
x+--3- 8- q = x− 3 = 2 = 4.

Pozostało uzasadnić podaną nierówność. Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy

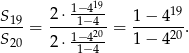
1−419 19 S19-= 2⋅--1−-4- = 1-−-4--. S20 2⋅ 1−420 1 − 420 1− 4

Będziemy teraz przekształcać (przy pomocy równoważności) podaną w zadaniu nierówność.

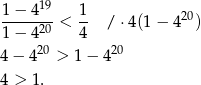
1 − 4 19 1 ------- < -- / ⋅4(1− 420) 1 − 4 20 4 4 − 420 > 1 − 420 4 > 1.

Otrzymaliśmy prawdziwą nierówność, więc ponieważ nasze przekształcenia były równoważnościami, wyjściowa nierówność też jest prawdziwa.  
Odpowiedź: q = 4

Wersja PDF