Zadanie nr 1849768
Metalowy walec o objętości 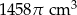 i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
Rozwiązanie
Szkicujemy walec i stożek.
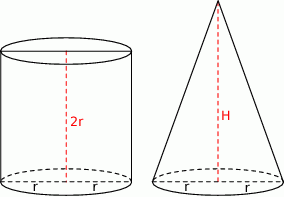
Jeżeli przez  oznaczymy promień podstawy walca i stożka, to wysokość walca jest równa
oznaczymy promień podstawy walca i stożka, to wysokość walca jest równa 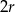 i z podanej objętości mamy
i z podanej objętości mamy
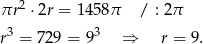
Objętości stożka i walca są równe, więc jeżeli przez 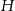 oznaczymy wysokość stożka, to mamy
oznaczymy wysokość stożka, to mamy
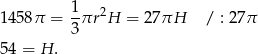
Obliczamy teraz długość tworzącej stożka.
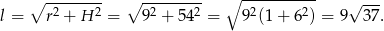
Pole powierzchni bocznej stożka jest więc równe
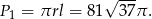
Pole powierzchni bocznej walca jest równe
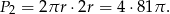
Interesujący nas stosunek pól jest więc równy
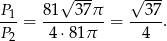
Odpowiedź: