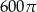/Szkoła średnia/Geometria/Stereometria/Stożek/Pole powierzchni

Zadanie nr 2027989

Objętość stożka jest równa 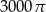3000π , a tworząca jest nachylona do podstawy pod kątem 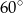60∘ . Oblicz pole powierzchni bocznej tego stożka.

Wersja PDF

Rozwiązanie

Szkicujemy stożek.

PIC

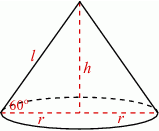
Obliczamy wysokość i tworzącą stożka w zależności od promienia podstawy.

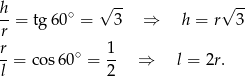
-- -- h-= tg6 0∘ = √ 3 ⇒ h = r√ 3 r r ∘ 1 - = cos6 0 = -- ⇒ l = 2r. l 2

Wykorzystujemy teraz informację o objętości stożka.

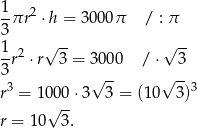
1- 2 3πr ⋅h = 3000π / : π 1 √ -- √ -- -r2 ⋅r 3 = 3000 / ⋅ 3 3 √ -- √ -- r3 = 1 000⋅ 3 3 = (10 3 )3 √ -- r = 10 3.

Mamy zatem 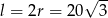√ -- l = 2r = 20 3 i pole powierzchni bocznej stożka jest równe

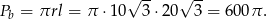
√ -- √ -- Pb = πrl = π ⋅10 3 ⋅20 3 = 600π .

 
Odpowiedź: 600 π

Wersja PDF