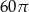/Szkoła średnia/Geometria/Stereometria/Stożek/Pole powierzchni

Zadanie nr 5228001

Dodaj do ulubionych
Dodaj do rozwiązanych

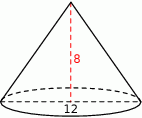
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.

PIC

Rozwiązanie

Z obrazka widać, że promień podstawy stożka jest równy połowie podstawy trójkąta, czyli 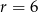r = 6 . Zatem tworząca ma długość (twierdzenie Pitagorasa)

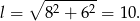
∘ ------- l = 82 + 6 2 = 10.

Pole powierzchni bocznej jest równe

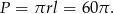
P = πrl = 60 π.

 
Odpowiedź: 60π

Wersja PDF