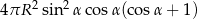/Szkoła średnia/Geometria/Stereometria/Stożek/Pole powierzchni

Zadanie nr 9199460

Dodaj do ulubionych
Dodaj do rozwiązanych

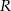Tworząca stożka jest nachylona do podstawy pod kątem α . Kula opisana na tym stożku ma promień R . Oblicz pole powierzchni całkowitej tego stożka.

Rozwiązanie

Narysujmy przekrój opisanej sytuacji

PIC

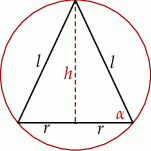
Na mocy twierdzenia sinusów

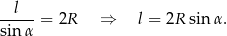
--l-- = 2R ⇒ l = 2R sin α. sin α

Liczymy dalej

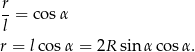
r - = cos α l r = lcosα = 2R sinα cos α.

Możemy teraz obliczyć szukane pole powierzchni

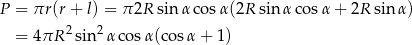
P = πr (r+ l) = π 2R sinα cos α(2R sinα cos α+ 2R sinα ) = 4πR 2sin 2α cosα (cosα + 1)

 
Odpowiedź: 2 2 4πR sin α cosα (cosα + 1 )

Wersja PDF