/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Prostokąt

Zadanie nr 1284651

Dodaj do ulubionych
Dodaj do rozwiązanych

Współrzędne przeciwległych wierzchołków prostokąta 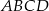ABCD są równe 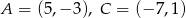A = (5,− 3), C = (− 7,1) . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 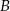B leży na prostej y = 5 .

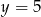Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

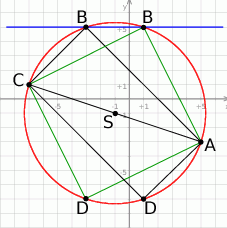
Sposób I

Skoro trójkąt 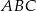ABC jest prostokątny, to punkt 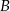B musi leżeć na okręgu o średnicy 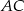AC . Środek 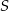S tego odcinka ma współrzędne

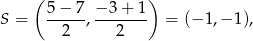
( ) S = 5-−-7, −3-+-1- = (− 1,− 1), 2 2

a promień jest równy

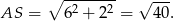
∘ ------- √ --- AS = 62 + 22 = 40.

Szukamy teraz punktów wspólnych okręgu

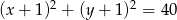
(x+ 1)2 + (y+ 1)2 = 40

i prostej 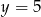y = 5 . Wstawiamy 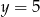y = 5 do równania okręgu.

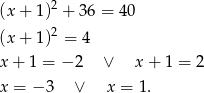
2 (x + 1) + 36 = 40 (x + 1)2 = 4 x + 1 = − 2 ∨ x + 1 = 2 x = − 3 ∨ x = 1.

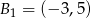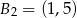Daje to nam dwa możliwe punkty B1 = (− 3,5) i B 2 = (1,5) . Odpowiadające punkty 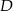D wyliczamy korzystając z tego, że 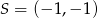S = (− 1,− 1) jest środkiem odcinka 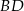BD . Mamy więc 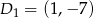D 1 = (1,− 7) i D 2 = (− 3,− 7) .

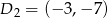Sposób II

Zamiast bawić się w okręgi, mogliśmy od razu skorzystać z twierdzenia Pitagorasa. Jeżeli oznaczymy 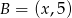B = (x,5) to mamy

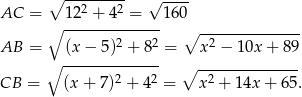
∘ ---2---2- √ ---- AC = ∘ 12--+-4--=----160 2 2 ∘ -2------------ AB = (x − 5) + 8 = x − 10x + 89 ∘ -------------- ∘ -------------- CB = (x + 7)2 + 42 = x 2 + 1 4x+ 65.

Korzystamy teraz z twierdzenia Pitagorasa

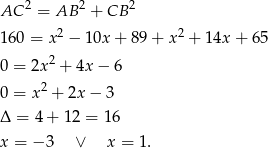
AC 2 = AB 2 + CB 2 2 2 160 = x − 10x + 89+ x + 14x + 65 0 = 2x2 + 4x − 6 2 0 = x + 2x − 3 Δ = 4 + 12 = 16 x = − 3 ∨ x = 1.

Współrzędne punktu 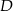D obliczamy jak poprzednio.

Sposób III

Tak jak w II sposobie szukamy punktu 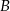B w postaci 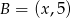B = (x,5) . Warunek 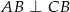AB ⊥ CB możemy zapisać przy pomocy iloczynu skalarnego.

− → −→ 0 = AB ∘ CB = [x− 5,5+ 3]∘ [x + 7,5− 1] 0 = [x − 5,8]∘ [x + 7,4] = (x − 5)(x + 7) + 8 ⋅4 0 = x2 + 2x − 3 5+ 32 2 0 = x − 2x − 3 .

Liczymy wyróżnik i pierwiastki

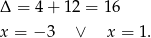
Δ = 4 + 12 = 16 x = − 3 ∨ x = 1.

Współrzędne punktu 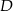D obliczamy jak poprzednio.  
Odpowiedź: 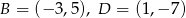B = (− 3,5), D = (1 ,−7 ) lub B = (1,5), D = (− 3,− 7)

Wersja PDF