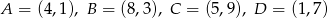/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Prostokąt

Zadanie nr 1913395

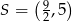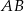Punkt ( 9 ) S = 2,5 jest środkiem symetrii prostokąta ABCD , którego pole jest równe 30, a bok AB jest zawarty w prostej o równaniu 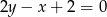2y − x+ 2 = 0 . Oblicz współrzędne wierzchołków prostokąta ABCD .

Wersja PDF

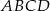Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

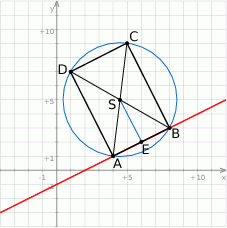
Zauważmy, że korzystając ze wzoru na odległość punktu od prostej łatwo jest obliczyć długość boku 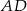AD prostokąta. Jak to zrobimy, to z podanego pola obliczymy długość drugiego boku prostokąta. Mamy zatem

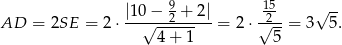
|1 0− 9+ 2| 15- √ -- AD = 2SE = 2⋅ --√---2-----= 2⋅ √2--= 3 5. 4 + 1 5

Z podanego pola mamy więc

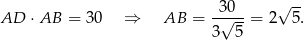
√ -- AD ⋅AB = 30 ⇒ AB = -3√0--= 2 5. 3 5

Zauważmy teraz, że łatwo obliczyć długość odcinka 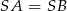SA = SB – jest to po prostu połowa długości przekątnej prostokąta.

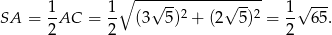
∘ ------------------ 1- 1- √ --2 √ --2 1-√ --- SA = 2AC = 2 (3 5) + (2 5) = 2 65.

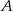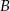Punkty A i B możemy teraz wyznaczyć jako punkty wspólne prostej 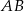AB oraz okręgu o środku 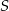S i promieniu 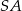SA . Rozwiązujemy więc układ równań

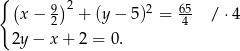
{ ( 9)2 2 65 x − 2 + (y− 5) = 4 / ⋅4 2y − x + 2 = 0.

Podstawiamy 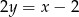2y = x − 2 z drugiego równania do pierwszego.

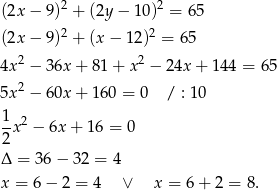
(2x − 9)2 + (2y − 10 )2 = 65 2 2 (2x − 9) + (x − 12) = 65 2 2 4x − 36x + 81+ x − 24x + 144 = 65 5x2 − 60x + 160 = 0 / : 10 1-x2 − 6x + 16 = 0 2 Δ = 36 − 32 = 4 x = 6 − 2 = 4 ∨ x = 6 + 2 = 8.

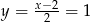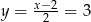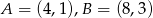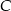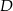Stąd odpowiednio x−2- y = 2 = 1 i x−2- y = 2 = 3 . Zatem A = (4,1),B = (8,3) . Współrzędne punktów C i D obliczamy ze wzoru na środek odcinka.

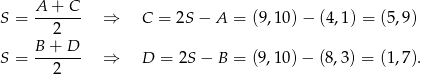
S = A-+--C- ⇒ C = 2S − A = (9,10)− (4,1) = (5,9) 2 B-+-D-- S = 2 ⇒ D = 2S− B = (9 ,10)− (8,3) = (1,7).

 
Odpowiedź: A = (4,1), B = (8 ,3 ), C = (5,9), D = (1,7)

Wersja PDF