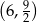Zadanie nr 2640905
Dane są dwa przeciwległe wierzchołki 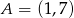 i
i 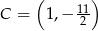 prostokąta
prostokąta 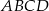 . Prosta o równaniu
. Prosta o równaniu 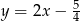 jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków
jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków 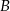 i
i 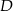 tego prostokąta.
tego prostokąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
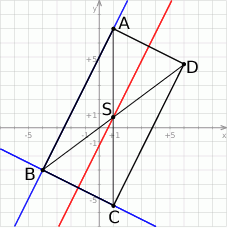
Napiszmy najpierw równanie prostej 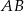 (przy oznaczeniach z powyższego rysunku). Szukamy prostej w postaci
(przy oznaczeniach z powyższego rysunku). Szukamy prostej w postaci 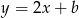 (równoległej do danej osi symetrii) i podstawiamy współrzędne punktu
(równoległej do danej osi symetrii) i podstawiamy współrzędne punktu 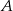
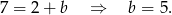
Prosta 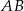 ma więc równanie
ma więc równanie 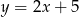 . Napiszemy teraz równanie prostej
. Napiszemy teraz równanie prostej 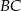 – szukamy prostej w postaci
– szukamy prostej w postaci 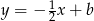 (prostopadłej do danej osi symetrii) i podstawiamy współrzędne punktu
(prostopadłej do danej osi symetrii) i podstawiamy współrzędne punktu 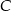 .
.
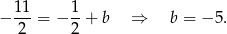
Prosta 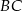 ma więc równanie
ma więc równanie 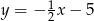 . Szukamy teraz punktu wspólnego
. Szukamy teraz punktu wspólnego 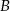 prostych
prostych 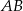 i
i 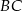 .
.
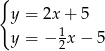
Odejmujemy od pierwszego równania drugie i mamy
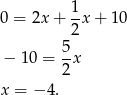
Stąd 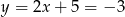 i
i 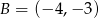 . Współrzędne punktu
. Współrzędne punktu 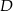 moglibyśmy wyznaczyć w podobny sposób – pisząc równania prostych
moglibyśmy wyznaczyć w podobny sposób – pisząc równania prostych  i
i 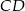 , ale my zrobimy to prościej, korzystając z tego, że środek prostokąta
, ale my zrobimy to prościej, korzystając z tego, że środek prostokąta
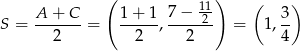
jest środkiem odcinka 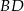 . Mamy zatem
. Mamy zatem
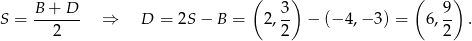
Odpowiedź: 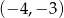 i
i