/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Prostokąt

Zadanie nr 3142193

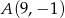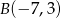Dane są dwa wierzchołki A (9,− 1) i B (−7 ,3) prostokąta 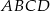ABCD oraz punkt 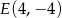E (4,− 4) należący do boku CD.

  • Wyznacz równanie prostej zawierającej bok CD ;
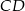  • Oblicz współrzędne wierzchołka C;
  • Oblicz współrzędne punktu 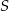S przecięcia się przekątnych tego prostokąta.
Wersja PDF

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

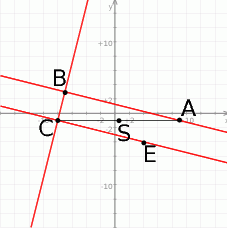
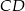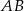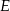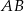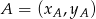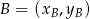  • Prosta CD jest równoległa do AB i przechodzi przez E . Zacznijmy od równania prostej AB . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA) i B = (xB,yB ) :
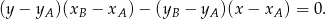
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    W naszej sytuacji mamy

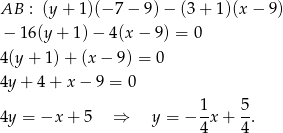
    AB : (y + 1)(− 7 − 9)− (3+ 1)(x − 9) − 16(y + 1) − 4(x − 9) = 0 4(y + 1) + (x − 9) = 0 4y + 4 + x − 9 = 0 1 5 4y = −x + 5 ⇒ y = − --x + -. 4 4

    Zatem prosta 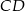CD jest postaci 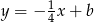y = − 14 x+ b . Współczynnik 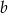b wyznaczmy z warunku, że przechodzi ona przez punkt E .

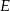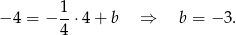
    1 − 4 = − --⋅4+ b ⇒ b = − 3. 4

    Zatem

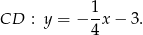
    1 CD : y = − --x− 3. 4

     
    Odpowiedź: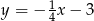 y = − 1x − 3 4

  • Napiszemy równanie prostej 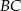BC – jest to prosta prostopadła do 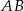AB i przechodząca przez 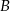B ; punkt 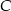C jest punktem wspólnym tych prostych.

    Prosta 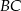BC jest prostopadła do prostej 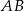AB , zatem jest postaci 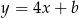y = 4x + b . Współczynnik 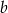b wyznaczmy z warunku, że przechodzi ona przez punkt B .

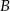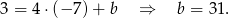
    3 = 4 ⋅(− 7)+ b ⇒ b = 31 .

    Zatem

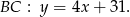
    BC : y = 4x+ 31.

    Punkt 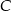C jest punktem wspólnym prostych 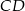CD i BC .

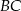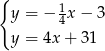
    { 1 y = − 4x− 3 y = 4x + 31

    Odejmując od drugiego równania pierwsze (żeby skrócić 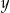y ) mamy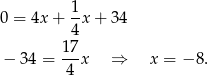

    0 = 4x+ 1x + 34 4 17- − 34 = 4 x ⇒ x = − 8.

    Z pierwszego równania mamy więc

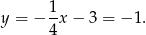
    y = − 1-x− 3 = − 1. 4

     
    Odpowiedź: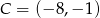 C = (− 8,− 1)

  • Punkt 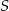S jest środkiem odcinka AC .
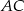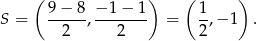
    ( ) ( ) S = 9-−-8-, −-1−-1 = 1,− 1 . 2 2 2

 
Odpowiedź: ( ) S = 12,− 1

Wersja PDF