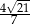Zadanie nr 1971681
Każda krawędź graniastosłupa prawidłowego trójkątnego  ma długość 4 (zobacz rysunek).
ma długość 4 (zobacz rysunek).
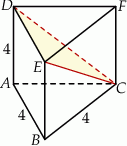
Oblicz odległość wierzchołka  tego graniastosłupa od płaszczyzny
tego graniastosłupa od płaszczyzny 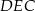 .
.
Rozwiązanie
Niech 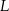 będzie rzutem punktu
będzie rzutem punktu 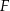 ma płaszczyznę
ma płaszczyznę  .
.
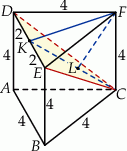
Punkt ten leży na wysokości 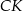 trójkąta równoramiennego
trójkąta równoramiennego 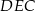 . Odcinek
. Odcinek 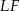 jest też wysokością trójkąta prostokątnego
jest też wysokością trójkąta prostokątnego 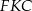 . Liczymy kolejno
. Liczymy kolejno
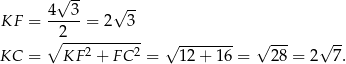
Liczymy teraz na dwa sposoby pole trójkąta 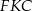 .
.
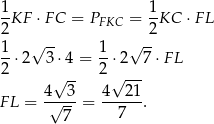
Odpowiedź: