Zadanie nr 3026341
Dany jest graniastosłup prawidłowy trójkątny 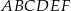 o podstawach
o podstawach 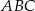 i
i 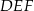 i krawędziach bocznych
i krawędziach bocznych 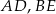 i
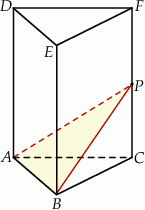
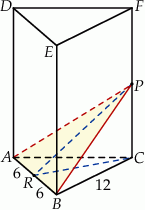
i 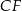 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 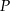 jest środkiem krawędzi
jest środkiem krawędzi 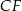 . Długość krawędzi podstawy
. Długość krawędzi podstawy 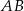 jest równa 12, a pole trójkąta
jest równa 12, a pole trójkąta 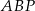 jest równe
jest równe 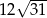 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Dorysujmy wysokości 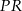 i
i 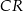 trójkątów
trójkątów 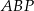 i
i 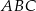 .
.
Z podanego pola przekroju obliczamy długość odcinka 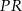 .
.
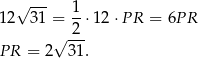
Ze wzoru na wysokość w trójkącie równobocznym mamy
Korzystając z twierdzenia Pitagorasa w trójkącie 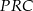 obliczamy długość odcinka
obliczamy długość odcinka 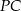 .
.
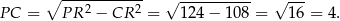
Pozostało obliczyć objętość graniastosłupa – korzystamy ze wzoru na pole trójkąta równobocznego.
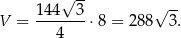
Odpowiedź: