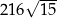Zadanie nr 3659242
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 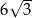 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 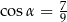 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Rozwiązanie
Zaczynamy od rysunku.
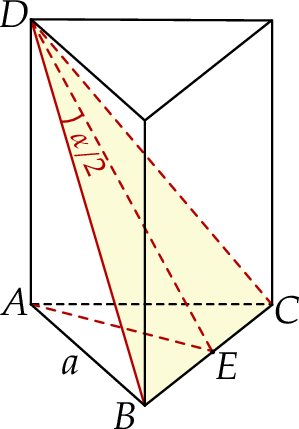
Jeżeli oznaczymy długość krawędzi podstawy przez  , to z podanej wysokości podstawy mamy
, to z podanej wysokości podstawy mamy
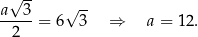
Sposób I
Aby móc wykorzystać trójkąt 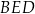 musimy znać
musimy znać 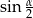 . Można go łatwo obliczyć z podanego cosinusa i wzoru na cosinus podwojonego kąta.
. Można go łatwo obliczyć z podanego cosinusa i wzoru na cosinus podwojonego kąta.
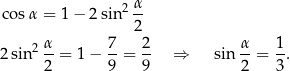
Patrzymy teraz na trójkąt 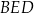 .
.
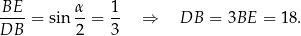
Patrzymy teraz na trójkąt 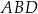
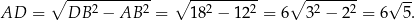
Liczymy teraz objętość
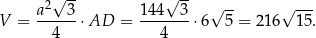
Sposób II
Długość odcinka 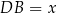 mogliśmy też obliczyć z twierdzenia cosinusów w trójkącie
mogliśmy też obliczyć z twierdzenia cosinusów w trójkącie 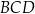 – nie musimy wtedy się bawić w kąty połówkowe.
– nie musimy wtedy się bawić w kąty połówkowe.
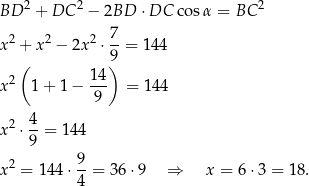
Dalej liczymy jak poprzednio.
Sposób III
Jeszcze inny sposób to skorzystanie ze związku cosinusa i tangensa połowy kąta.
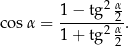
Wzór ten można znaleźć w tablicach. Mamy wtedy
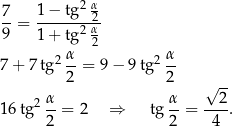
To nam pozwala łatwo obliczyć długość odcinka 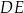 .
.
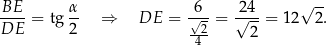
Stąd
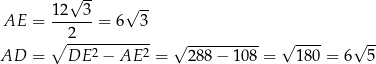
Objętość liczymy tak samo jak w pierwszym sposobie.
Sposób IV
Niech 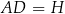 będzie wysokością graniastosłupa. W trójkącie prostokątnym
będzie wysokością graniastosłupa. W trójkącie prostokątnym 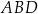 mamy wtedy
mamy wtedy
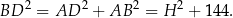
Stąd
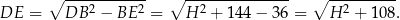
Zauważmy jeszcze, że
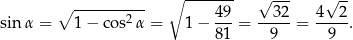
Obliczyliśmy  , bo chcemy skorzystać ze wzoru na pole z sinusem w trójkącie
, bo chcemy skorzystać ze wzoru na pole z sinusem w trójkącie  . Mamy zatem
. Mamy zatem
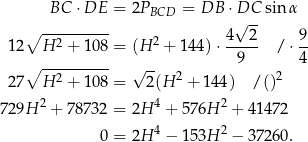
Otrzymaliśmy równanie dwukwadratowe, więc podstawiamy 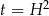 i mamy
i mamy
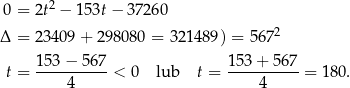
Mamy zatem 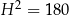 , czyli
, czyli 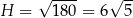 . Objętość graniastosłupa jest więc równa
. Objętość graniastosłupa jest więc równa
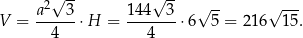
Odpowiedź: