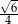/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 3813312

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 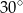30 ∘ .

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

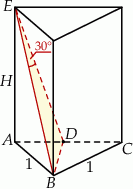
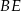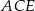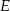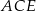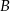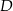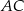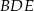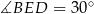Aby zaznaczyć kąt jaki tworzy przekątna BE ściany bocznej z sąsiednią ścianą ACE , musimy znaleźć rzut tej przekątnej na tę ścianę. Nie jest to trudne – wystarczy popatrzeć gdzie wylądują końce przekątnej. Punkt E jest już na ścianie ACE , a punkt B przejdzie na środek D krawędzi AC . Otrzymamy w ten sposób trójkąt prostokątny BDE , w którym ∡BED = 30∘ .

Ponieważ 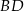BD jest wysokością w trójkącie równobocznym w podstawie, mamy

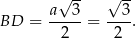
√ -- √ -- a 3 3 BD = ----- = ----. 2 2

Z trójkąta 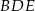BDE wyliczamy długość przekątnej 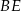BE ściany bocznej.

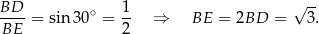
BD-- ∘ 1- √ -- BE = sin 30 = 2 ⇒ BE = 2BD = 3 .

Teraz możemy wyliczyć długość wysokości 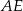AE graniastosłupa. Patrzymy na trójkąt prostokątny ABE .

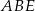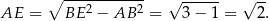
∘ ------------ 2 2 √ ------ √ -- AE = BE − AB = 3 − 1 = 2.

Zatem objętość graniastosłupa jest równa

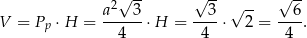
2√ -- √ -- √ -- √ -- V = Pp ⋅H = a---3-⋅H = --3⋅ 2 = --6-. 4 4 4

 
Odpowiedź: √ - -46

Wersja PDF