/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 4919014

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 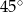45∘ . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 16 √ 3- .

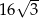Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

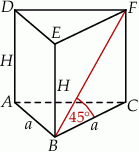
Zauważmy, że trójkąt 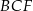BCF jest prostokątny z kątem 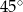45 ∘ , więc jest połówką kwadratu. W takim razie ściany boczne graniastosłupa to kwadraty. Jeżeli oznaczymy bok tych kwadratów przez a , to z podanej objętości mamy

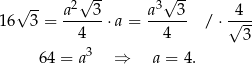
-- -- √ -- a2√ 3 a3√ 3 4 16 3 = ------⋅a = ------ / ⋅√--- 4 4 3 64 = a 3 ⇒ a = 4.

Pole powierzchni bocznej jest więc równe

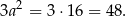
2 3a = 3⋅1 6 = 48.

 
Odpowiedź: 48

Wersja PDF