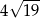/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 5721672

Dodaj do ulubionych
Dodaj do rozwiązanych

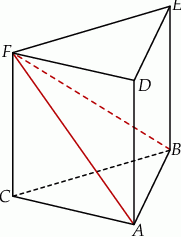
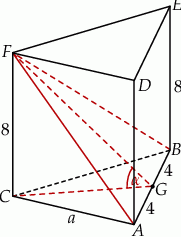
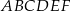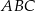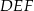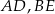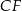Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych AD ,BE i CF (zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 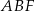ABF poprowadzoną z wierzchołka 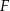F i płaszczyzną podstawy 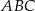ABC tego graniastosłupa jest równy 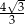4√3 -3-- . Oblicz pole trójkąta ABF .

PIC

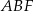Rozwiązanie

Zauważmy, że trójkąt 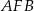AF B jest równoramienny więc jego wysokość 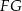FG opuszczona z wierzchołka 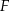F dzieli krawędź 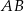AB na połowy.

PIC

Z podanego tangensa kąta 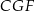CGF mamy

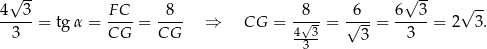
√ -- √ -- 4--3-= tg α = -FC- = -8-- ⇒ CG = -8√--= √6--= 6--3-= 2√ 3. 3 CG CG 4-3- 3 3 3

Jeżeli oznaczmy przez a długość boku trójkąta równobocznego w podstawie graniastosłupa, to ze wzoru na wysokość w trójkącie równobocznym mamy

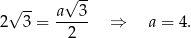
-- √ -- a √ 3 2 3 = ----- ⇒ a = 4 . 2

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 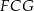FCG .

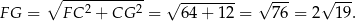
∘ ---2------2- √ -------- √ --- √ --- F G = F C + CG = 6 4+ 1 2 = 76 = 2 19.

Pozostało obliczyć pole trójkąta 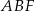ABF .

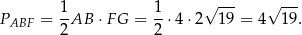
1 1 √ --- √ --- PABF = --AB ⋅FG = --⋅4 ⋅2 19 = 4 19. 2 2

 
Odpowiedź: √ --- 4 19

Wersja PDF