/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 5777791

Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem 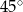45 ∘ do dolnej podstawy. Pole otrzymanego przekroju wynosi 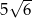√ -- 5 6 . Oblicz objętość tego graniastosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

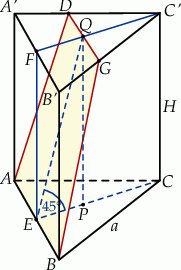
Przekrój, o którym mowa w zadaniu jest trapezem równoramiennym. Widać, że z podanego kąta nachylenia tego przekroju możemy uzależnić wysokość graniastosłupa 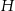H w zależności od długości jego krawędzi podstawy a .

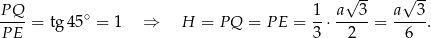
-- -- P Q 1 a√ 3 a√ 3 ---- = tg 45∘ = 1 ⇒ H = PQ = P E = --⋅ -----= ----. PE 3 2 6

Skorzystaliśmy ze wzoru na długość wysokości w trójkącie równobocznym oraz faktu, że środek trójkąta równobocznego dzieli jego wysokości w stosunku 2:1.

Trójkąt 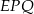EP Q jest połówką kwadratu, więc

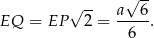
√ -- √ -- EQ = EP 2 = a---6. 6

Do wyliczenia pola przekroju brakuje nam jeszcze długości podstawy 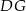DG . Jak już napisaliśmy, środek ciężkości 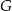G dzieli wysokość 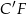C′F w stosunku 2:1, więc

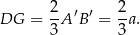
DG = 2-A′B ′ = 2a. 3 3

Możemy teraz policzyć pole trapezu.

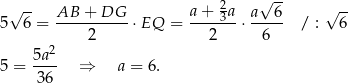
√ -- a + 2a √ -- √ -- 5 6 = AB--+-DG--⋅EQ = ----3--⋅ a--6- / : 6 2 2 6 5a2 5 = ---- ⇒ a = 6 . 36

Pozostało policzyć objętość.

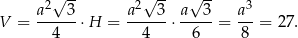
√ -- √ -- √ -- a2 3 a2 3 a 3 a3 V = -----⋅ H = ------⋅-----= ---= 27. 4 4 6 8

 
Odpowiedź: 27

Wersja PDF