Zadanie nr 6437886
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy równej 6, poprowadzono płaszczyznę przechodzącą przez wysokość podstawy oraz wierzchołek górnej podstawy. Wiedząc, że płaszczyzna ta tworzy z płaszczyzną podstawy kąt o mierze 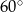 oblicz pole otrzymanego przekroju.
oblicz pole otrzymanego przekroju.
Rozwiązanie
Rozpoczynamy od rysunku.
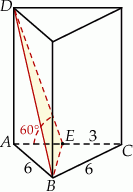
Płaszczyzna 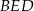 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 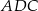 (bo zawiera prostą
(bo zawiera prostą 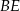 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny 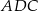 ). Zatem trójkąt
). Zatem trójkąt 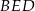 jest prostokątny, a podany kąt między płaszczyzną przekroju i płaszczyzną podstawy to kąt
jest prostokątny, a podany kąt między płaszczyzną przekroju i płaszczyzną podstawy to kąt 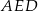 . Aby obliczyć pole otrzymanego przekroju musimy obliczyć długości przyprostokątnych
. Aby obliczyć pole otrzymanego przekroju musimy obliczyć długości przyprostokątnych 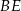 i
i 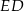 trójkąta
trójkąta 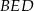 . Z pierwszą nie ma problemu – jest to wysokość w trójkącie równobocznym
. Z pierwszą nie ma problemu – jest to wysokość w trójkącie równobocznym 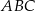 .
.
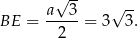
Drugą przyprostokątną wyliczamy z trójkąta 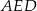
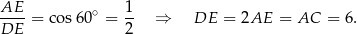
Zatem pole przekroju jest równe
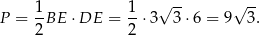
Odpowiedź: