Zadanie nr 6809237
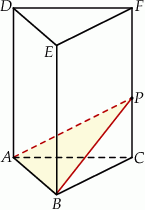
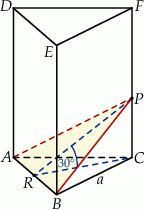
Dany jest graniastosłup prawidłowy trójkątny 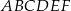 o podstawach
o podstawach 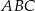 i
i 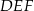 i krawędziach bocznych
i krawędziach bocznych 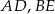 i
i 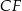 (zobacz rysunek). Przez krawędź
(zobacz rysunek). Przez krawędź 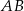 poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem
poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem 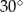 . Płaszczyzna ta przecina krawędź
. Płaszczyzna ta przecina krawędź 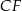 w punkcie
w punkcie 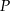 . Oblicz pole trójkąta
. Oblicz pole trójkąta 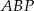 jeżeli objętość ostrosłupa
jeżeli objętość ostrosłupa 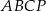 jest równa
jest równa 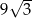 .
.
Rozwiązanie
Dorysujmy wysokości 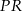 i
i 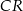 trójkątów
trójkątów 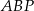 i
i 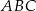 oraz oznaczmy krawędź podstawy przez
oraz oznaczmy krawędź podstawy przez  .
.
W trójkącie prostokątnym 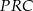 mamy
mamy
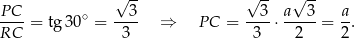
Korzystamy teraz z podanej objętości ostrosłupa  .
.
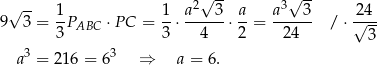
Patrzymy jeszcze raz na trójkąt 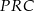 – obliczamy z niego wysokość
– obliczamy z niego wysokość 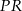 trójkąta
trójkąta 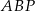 .
.
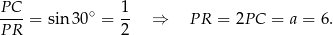
Pole trójkąta 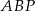 jest więc równe
jest więc równe
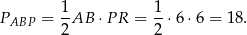
Odpowiedź: 18

