Zadanie nr 7244139
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
Rozwiązanie
Zacznijmy od rysunku.
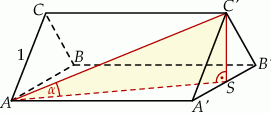
Rysunek specjalnie narysowaliśmy trochę nietypowo (graniastosłup leży na ścianie bocznej) – dzięki temu lepiej widać jak wygląda rzut przekątnej ściany bocznej na sąsiednią ścianę, w szczególności widać, że rzut 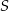 wierzchołka
wierzchołka 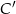 to środek krawędzi
to środek krawędzi 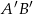 .
.
Powinno być jasne, że podany warunek wyznacza jednoznacznie graniastosłup z dokładnością do skali, tzn. wyznacza kształt graniastosłupa. Mówiąc dokładniej, z dokładnością do skali, graniastosłup jest wyznaczony przez stosunek wysokości do krawędzi podstawy. Jest jasne, że tylko dla jednego takiego stosunku będzie spełniony podany warunek. Takie przemyślenia nie są niezbędne do rozwiązania zadania, ale dobrze jest wiedzieć co jest grane – dlaczego szukany tangens da się wyliczyć, pomimo, że nie jest podana żadna wartość liczbowa.
Ponieważ zmiana skali nie zmienia treści zadania (tzn. nie zmienia ani założeń ani tezy), możemy sobie założyć, że krawędź podstawy ma długość 1. Jeżeli ktoś nie jest przekonany, że można tak zrobić, to może sobie założyć, że ta krawędź ma długość  i wszystkie wyliczone przez nas długości odcinków będzie musiał pomnożyć przez
i wszystkie wyliczone przez nas długości odcinków będzie musiał pomnożyć przez  .
.
Pole powierzchni bocznej to suma pól trzech prostokątów o polu 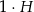 , gdzie
, gdzie 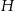 – wysokość graniastosłupa, czyli pole powierzchni bocznej jest równe
– wysokość graniastosłupa, czyli pole powierzchni bocznej jest równe 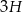 . Suma pól podstaw to suma pól dwóch trójkątów równobocznych o boku 1, mamy więc równanie
. Suma pól podstaw to suma pól dwóch trójkątów równobocznych o boku 1, mamy więc równanie
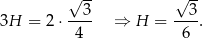
Liczymy teraz długość odcinka 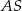
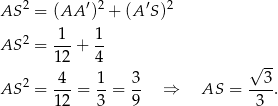
Odcinek 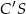 to wysokość w trójkącie równobocznym, zatem
to wysokość w trójkącie równobocznym, zatem
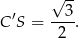
Możemy więc wyliczyć szukany tangens
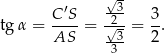
Odpowiedź: 

