/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 7319700

Dodaj do ulubionych
Dodaj do rozwiązanych

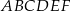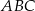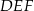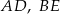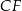Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych AD , BE i CF , które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta 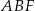ABF stanowi 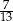7- 13 pola ściany bocznej ABED .

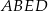Rozwiązanie

Rozpoczynamy od rysunku.

PIC

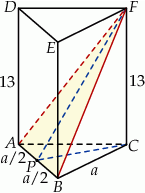
Widać, że trójkąt 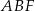ABF jest równoramienny – oznaczmy długość jego podstawy przez a . Rozpoczniemy od zapisania podanej informacji o stosunku pól powierzchni.

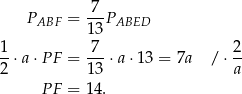
-7- PABF = 13 PABED 1 7 2 --⋅a ⋅P F = ---⋅a ⋅13 = 7a / ⋅-- 2 13 a P F = 14.

Teraz piszemy twierdzenie Pitagorasa w trójkącie 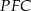P FC .

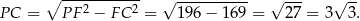
∘ ----------- √ ---------- √ --- √ -- P C = PF 2 − F C2 = 196− 169 = 2 7 = 3 3.

Korzystamy teraz ze wzoru na wysokość w trójkącie równobocznym.

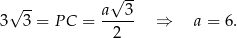
√ -- √ -- a--3- 3 3 = P C = 2 ⇒ a = 6.

Pozostało obliczyć pole powierzchni całkowitej

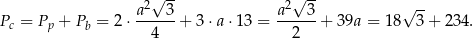
√ -- √ -- a2--3- a2--3- √ -- Pc = Pp + Pb = 2 ⋅ 4 + 3 ⋅a ⋅13 = 2 + 39a = 1 8 3+ 234.

oraz objętość

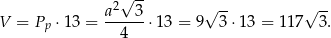
√ -- a2 3 √ -- √ -- V = Pp ⋅13 = ------⋅13 = 9 3 ⋅13 = 117 3. 4

 
Odpowiedź: 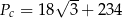√ -- Pc = 1 8 3+ 234 , √ -- V = 11 7 3

Wersja PDF