/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9014425

Krawędź podstawy graniastosłupa prawidłowego trójkątnego 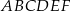ABCDEF jest równa 6 (zobacz rysunek). Punkt 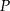P dzieli krawędź boczną 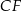CF w stosunku 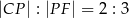|CP | : |P F| = 2 : 3 . Pole trójkąta 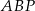ABP jest równe 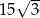√ -- 15 3 . Oblicz objętość tego graniastosłupa.

PIC

Wersja PDF

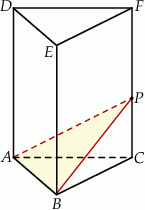
Rozwiązanie

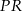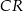Dorysujmy wysokości PR i CR trójkątów 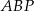ABP i ABC .

PIC

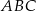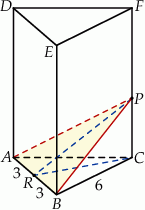
Z podanego pola przekroju obliczamy długość odcinka 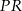P R .

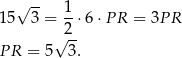
√ -- 1 5 3 = 1-⋅6 ⋅PR = 3P R √2-- P R = 5 3.

Ze wzoru na wysokość w trójkącie równobocznym mamy

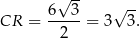
√ -- 6 3 √ -- CR = -----= 3 3. 2

Korzystamy z twierdzenia Pitagorasa w trójkącie 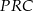PRC i obliczamy długość odcinka PC .

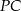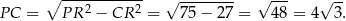
∘ ---2------2- √ -------- √ --- √ -- P C = PR − CR = 75 − 27 = 48 = 4 3.

Stąd 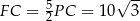5 √ -- FC = 2P C = 10 3 i objętość graniastosłupa jest równa

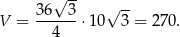
√ -- √ -- V = 36--3-⋅10 3 = 270. 4

 
Odpowiedź: 270

Wersja PDF