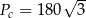/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9091691

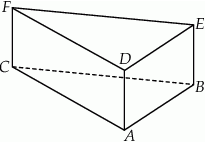
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Objętość tego graniastosłupa jest równa 324. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz pole powierzchni całkowitej tego graniastosłupa.

PIC

Wersja PDF

Rozwiązanie

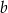Oznaczmy przez a długość krawędzi podstawy graniastosłupa, a przez b długość jego krawędzi bocznej. W takim razie pole podstawy jest równe

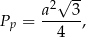
√ -- a2--3- Pp = 4 ,

a pole jednej ściany bocznej jest równe

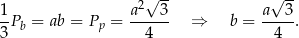
√ -- √ -- 1- a-2--3 a--3- 3Pb = ab = Pp = 4 ⇒ b = 4 .

Korzystamy teraz z podanej informacji o objętości graniastosłupa

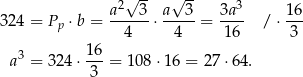
√ -- √ -- a2 3 a 3 3a 3 1 6 324 = Pp ⋅ b =--4---⋅--4-- = -16- / ⋅-3- a 3 = 324 ⋅ 16-= 108⋅ 16 = 27 ⋅64. 3

Zatem 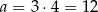a = 3 ⋅4 = 12 i pole powierzchni całkowitej graniastosłupa jest równe

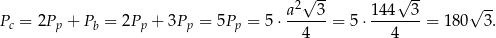
2√ -- √ -- P = 2P + P = 2P + 3P = 5P = 5 ⋅ a--3-= 5 ⋅ 144-3-= 180√ 3-. c p b p p p 4 4

 
Odpowiedź: √ -- Pc = 1 80 3

Wersja PDF