/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9187826

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 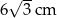√ -- 6 3 cm . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 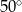50∘ . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.

Rozwiązanie

Zaczynamy od rysunku.

PIC

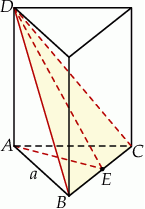
Jeżeli oznaczymy długość krawędzi podstawy przez a to mamy równanie

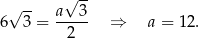
√ -- 6√ 3-= a--3- ⇒ a = 12. 2

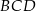Trójkąt BCD jest równoramienny, więc z trójkąta 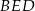BED mamy

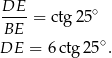
DE-- = ctg 25∘ BE DE = 6ctg 25∘.

Teraz z trójkąta 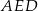AED możemy obliczyć wysokość AD .

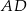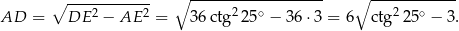
∘ ------------------- ∘ ------------ ∘ ---2------2- 2 ∘ 2 ∘ AD = DE − AE = 36ctg 25 − 36⋅ 3 = 6 ctg 25 − 3.

Zatem objętość i pole powierzchni całkowitej wynoszą odpowiednio

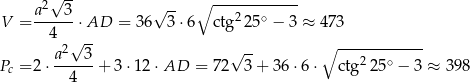
√ -- a2 3 √ -- ∘ ------------ V = ------⋅AD = 3 6 3⋅6 ctg225 ∘ − 3 ≈ 473 4 √ -- ∘ ------------ a2--3- √ -- 2 ∘ Pc = 2 ⋅ 4 + 3 ⋅12 ⋅AD = 72 3 + 36 ⋅6 ⋅ ctg 25 − 3 ≈ 398

 
Odpowiedź: 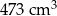3 47 3 cm i 2 3 98 cm

Wersja PDF