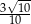/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9395695

Promień okręgu opisanego na podstawie graniastosłupa prawidłowego trójkątnego ma długość 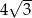√ -- 4 3 . Pole powierzchni bocznej jest równe 144.

  1. Oblicz objętość tego graniastosłupa.
  2. Oblicz cosinus kąta między przekątną ściany bocznej i krawędzią podstawy graniastosłupa.
Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

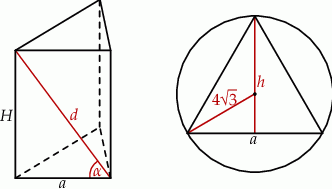
Promień okręgu opisanego na trójkącie równobocznym stanowi 23 wysokości tego trójkąta, czyli

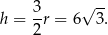
√ -- h = 3r = 6 3. 2

Obliczamy długość krawędzi podstawy

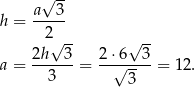
√ -- h = a--3- 2 2h√ 3- 2 ⋅6√ 3- a = ------= --√-----= 12. 3 3
  • Ze wzoru na pole boczne wyznaczamy wysokość graniastosłupa
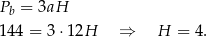
    Pb = 3aH 14 4 = 3⋅ 12H ⇒ H = 4.

    Teraz już łatwo policzyć objętość graniastosłupa

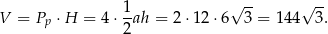
    1 √ -- √ -- V = Pp ⋅H = 4 ⋅-ah = 2⋅ 12⋅ 6 3 = 144 3 . 2

     
    Odpowiedź: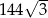 √ -- 144 3

  • Z twierdzenia Pitagorasa obliczamy długość przekątnej d
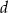
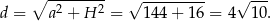
    ∘ -------- --------- --- d = a2 + H 2 = √ 144+ 16 = 4√ 1 0.

    Wyznaczamy cosinus

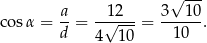
    √ --- a 12 3 10 co sα = d-= --√----= -10--. 4 10

     
    Odpowiedź: √-- 3-10- 10

Wersja PDF