/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9586181

Dodaj do ulubionych
Dodaj do rozwiązanych

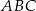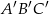Dany jest graniastosłup prawidłowy trójkątny o podstawach ABC i ′ ′ ′ A B C oraz krawędziach bocznych 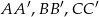AA ′,BB ′,CC ′ . Kąt nachylenia przekątnej ściany bocznej 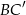BC ′ do płaszczyzny podstawy ma miarę α . Promień okręgu wpisanego w podstawę graniastosłupa ma długość r . Oblicz objętość tego graniastosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

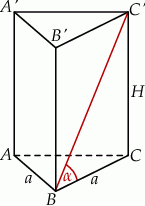
Z podanego promienia okręgu wpisanego w podstawę, możemy wyliczyć długość krawędzi podstawy. Promień okręgu wpisanego w trójkąt równoboczny to 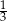1 3 wysokości tego trójkąta, czyli

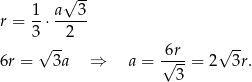
√ -- 1 a 3 r = --⋅----- 3√ --2 √ -- 6r = 3a ⇒ a = 6√r--= 2 3r. 3

Wysokość graniastosłupa wyliczamy z podanego kąta.

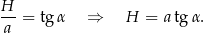
H- = tg α ⇒ H = a tgα . a

Liczymy teraz objętość (korzystamy ze wzoru na pole trójkąta równobocznego).

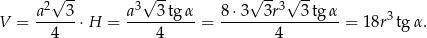
2√ -- 3√ -- √ --3√ -- V = a---3-⋅H = a---3-tg-α-= 8-⋅3--3r---3-tg-α-= 18r3tg α. 4 4 4

 
Odpowiedź: 3 18r tg α

Wersja PDF