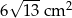/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny

Zadanie nr 9924137

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość 6 cm, a wysokość graniastosłupa jest równa 10 cm. Oblicz pole przekroju graniastosłupa płaszczyzną wyznaczoną przez krawędź podstawy i środek przeciwległej krawędzi bocznej.

Rozwiązanie

Zaczynamy od rysunku.

PIC

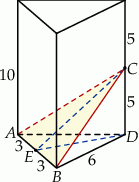
Otrzymany przekrój to trójkąt równoramienny o podstawie 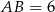AB = 6 . Aby obliczyć jego pole, musimy wyliczyć wysokość 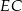EC . Zrobimy to z trójkąta prostokątnego EDC .

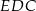Ze wzoru na wysokość w trójkącie równobocznym mamy

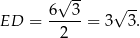
-- 6√ 3 √ -- ED = -----= 3 3. 2

Z twierdzenia Pitagorasa w trójkącie 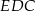EDC mamy

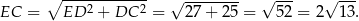
∘ ---2------2- √ -------- √ --- √ --- EC = ED + DC = 27+ 25 = 52 = 2 13.

Zatem pole przekroju jest równe

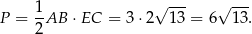
1 √ --- √ --- P = --AB ⋅EC = 3 ⋅2 13 = 6 13. 2

 
Odpowiedź: √ --- 2 6 13 cm

Wersja PDF