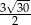W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.
Rozpoczynamy od rysunku.
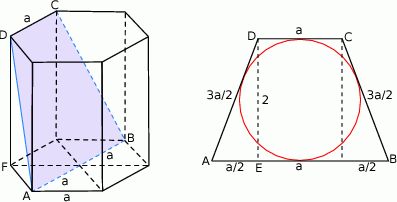
Oznaczmy długość krawędzi podstawy graniastosłupa przez 
.
Ponieważ podstawa graniastosłupa składa się z 6 trójkątów równobocznych, długość przekątnej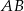 
jest równa 
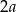. Zatem podstawy trapezu 
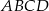mają długości 
i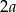 
. Jak wiemy, w trapez można wpisać okrąg, więc ramiona muszą mieć długości 
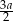(żeby sumy przeciwległych boków były równe). Ponadto
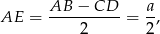
gdzie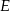 
jest spodkiem wysokości opuszczonej z wierzchołka 
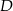. Piszemy teraz twierdzenie Pitagorasa w trójkącie 
.
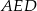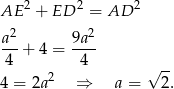
Zatem pole podstawy graniastosłupa jest równe
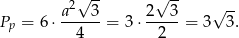
Wysokość graniastosłupa obliczamy z trójkąta prostokątnego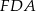 
.
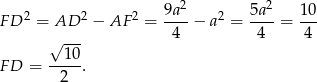
Liczymy objętość
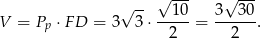
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
