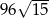Zadanie nr 5913383
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 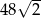 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy
. Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy 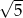 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Szkicujemy opisaną sytuację.
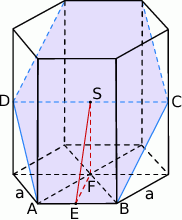
Niech  będzie długością krawędzi podstawy, a
będzie długością krawędzi podstawy, a 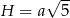 wysokością graniastosłupa. W szczególności, każda z podstaw graniastosłupa jest sześciokątem foremnym składającym się z 6 trójkątów równobocznych o boku
wysokością graniastosłupa. W szczególności, każda z podstaw graniastosłupa jest sześciokątem foremnym składającym się z 6 trójkątów równobocznych o boku  .
.
Przekrój, o którym mowa w treści zdania jest sześciokątem, którego dwa przeciwległe boki są krawędziami podstaw graniastosłupa, a dwa przeciwległe wierzchołki  są środkami krawędzi bocznych graniastosłupa. Sześciokąt ten składa się z dwóch przystających trapezów równoramiennych, więc
są środkami krawędzi bocznych graniastosłupa. Sześciokąt ten składa się z dwóch przystających trapezów równoramiennych, więc
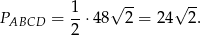
Zanim wykorzystamy tę informację spróbujmy wyznaczyć wysokość trapezu 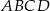 . W trójkącie prostokątnym
. W trójkącie prostokątnym 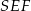 mamy
mamy
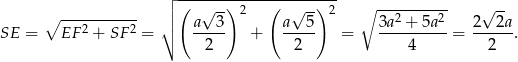
Ponadto dłuższa podstawa  trapezu
trapezu  ma taką samą długość jak dłuższa przekątna sześciokąta w podstawie graniastosłupa, czyli
ma taką samą długość jak dłuższa przekątna sześciokąta w podstawie graniastosłupa, czyli 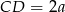 . Zapisujemy teraz podaną informację o polu trapezu
. Zapisujemy teraz podaną informację o polu trapezu 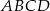 .
.
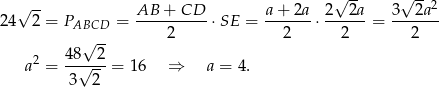
Objętość graniastosłupa jest więc równa
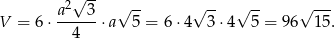
Odpowiedź: