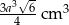Zadanie nr 7709252
Krawędź podstawy graniastosłupa prawidłowego sześciokątnego ma długość  . Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.
. Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Zaczynamy od rysunku.
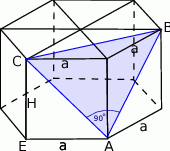
Z podanych informacji wiemy, że trójkąt 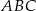 jest prostokątny. Jest on też równoramienny, więc jest to dokładnie połówka kwadratu. Zatem
jest prostokątny. Jest on też równoramienny, więc jest to dokładnie połówka kwadratu. Zatem
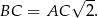
Z drugiej strony, jeżeli połączymy przeciwległe wierzchołki sześciokąta w górnej podstawie, to mamy sześć trójkątów równobocznych i widać, że odcinek 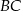 jest dwa razy dłuższy od wysokości każdego z tych trójkątów równobocznych, czyli
jest dwa razy dłuższy od wysokości każdego z tych trójkątów równobocznych, czyli
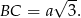
Mamy zatem
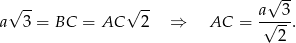
Teraz z trójkąta prostokątnego 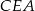 wyliczamy wysokość graniastosłupa.
wyliczamy wysokość graniastosłupa.
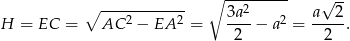
Możemy teraz policzyć objętość (korzystamy ze wzoru na pole trójkąta równobocznego).
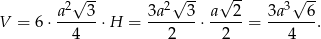
Odpowiedź: