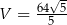/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny

Zadanie nr 1913769

Podstawą graniastosłupa prostego 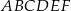ABCDEF jest trójkąt prostokątny 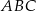ABC , w którym 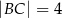|BC | = 4 . Promień okręgu opisanego na trójkącie 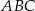ABC ma długość 3, a sinus kąta nachylenia przekątnej 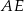AE ściany bocznej 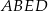ABED do płaszczyzny podstawy jest równy 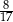-8 17 . Oblicz objętość tego graniastosłupa.

PIC

Wersja PDF

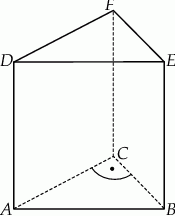
Rozwiązanie

Środek okręgu opisanego na trójkącie prostokątnym to dokładnie środek przeciwprostokątnej 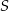S (przeciwprostokątna jest średnicą tego okręgu).

PIC

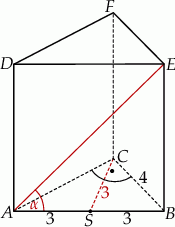
Zatem

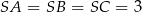
SA = SB = SC = 3

oraz

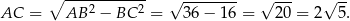
∘ ------------ √ -------- √ --- √ -- AC = AB 2 − BC 2 = 36 − 16 = 20 = 2 5 .

Z podanego sinusa kąta 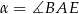α = ∡BAE obliczamy 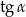tg α (żeby móc potem obliczyć wysokość ostrosłupa).

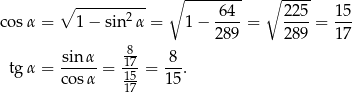
∘ -------- ∘ ---- ∘ -------2-- -64- 225- 15- cosα = 1 − sin α = 1 − 28 9 = 289 = 17 8- tgα = sinα- = -17 = -8-. cos α 15 15 17

Patrzymy teraz na trójkąt prostokątny 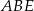ABE .

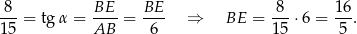
-8- BE-- BE- -8- 16- 1 5 = tg α = AB = 6 ⇒ BE = 15 ⋅6 = 5 .

Objętość graniastosłupa jest więc równa

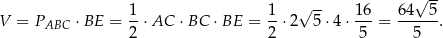
√ -- √ -- V = PABC ⋅BE = 1-⋅AC ⋅BC ⋅BE = 1-⋅2 5⋅4 ⋅ 1-6 = 64--5. 2 2 5 5

 
Odpowiedź: √ - V = 64--5 5

Wersja PDF