/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny

Zadanie nr 2257036

Dodaj do ulubionych
Dodaj do rozwiązanych

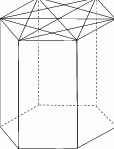
Liczba wszystkich przekątnych podstaw i ścian bocznych pewnego graniastosłupa jest równa 110. Oblicz, ile krawędzi ma podstawa tego graniastosłupa.

Rozwiązanie

Żeby policzyć przekątne podstaw, potrzebujemy wzór na ilość przekątnych n –kąta wypukłego.

PIC

Wzór taki można uzyskać na różne sposoby. Np. wszystkich par wierzchołków jest 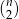(n2) , a przekątnych jest o n mniej, bo trzeba odjąć boki wielokąta. Przekątnych jest więc

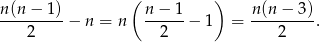
( ) n-(n−--1) n-−-1- n(n-−-3)- 2 − n = n 2 − 1 = 2 .

Inny sposób jest następujący: z każdego wierzchołka wychodzi 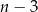n − 3 przekątnych (do wszystkich wierzchołków oprócz sąsiednich). Ponieważ wierzchołków jest n , to biorąc iloczyn 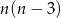n(n − 3) mamy wszystkie przekątne, ale liczymy je podwójnie (w jednym i w drugim wierzchołku). Zatem liczba wszystkich przekątnych jest równa

n-(n−--3) 2 .

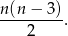
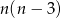Korzystając z tego wzoru wiemy, że jeżeli podstawą graniastosłupa jest n –kąt to w podstawach mamy n(n − 3) przekątnych. Do tego trzeba dodać przekątne ścian – to jest jednak łatwe, bo w ścianach są prostokąty, więc wszystkich przekątnych ścian będzie 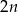2n . Mamy zatem równanie

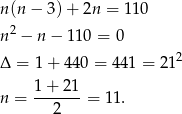
n (n− 3)+ 2n = 1 10 n 2 − n − 110 = 0 2 Δ = 1 + 440 = 441 = 21 1-+-21- n = 2 = 11.

 
Odpowiedź: 11

Wersja PDF