/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny

Zadanie nr 5548379

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prostego jest trójkąt 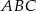ABC o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.

Rozwiązanie

Jak wykonamy rysunek, to jest jasne, że zadanie tak naprawdę nie jest przestrzenne – to co mamy wyliczyć to cosinusy kątów trójkąta ABC w podstawie.

PIC

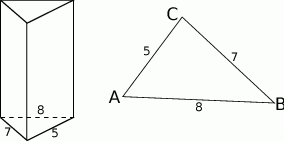
Cosinusy te bez trudu wyliczamy z twierdzenia cosinusów.

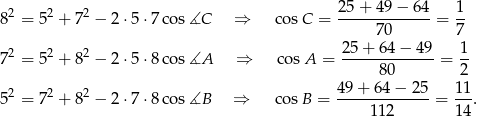
8 2 = 52 + 72 − 2 ⋅5 ⋅7co s∡C ⇒ cos C = 25+--49−--64-= 1- 70 7 2 2 2 25-+-64-−-49- 1- 7 = 5 + 8 − 2 ⋅5 ⋅8co s∡A ⇒ cos A = 80 = 2 4 9+ 6 4− 25 1 1 5 2 = 72 + 82 − 2 ⋅7 ⋅8co s∡B ⇒ cosB = ------------- = ---. 112 1 4

 
Odpowiedź: 1, 1, 11 7 2 14

Wersja PDF