Zadanie nr 6107689
Podstawą graniastosłupa prostego 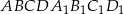 jest trapez równoramienny
jest trapez równoramienny 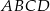 wpisany w okrąg o środku
wpisany w okrąg o środku 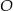 i promieniu
i promieniu 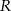 . Dłuższa podstawa
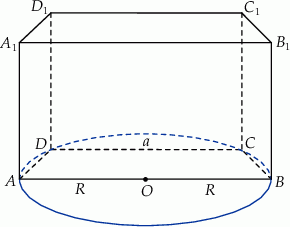
. Dłuższa podstawa 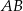 trapezu jest średnicą tego okręgu, a krótsza ma długość
trapezu jest średnicą tego okręgu, a krótsza ma długość  (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 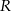 , długości podstawy
, długości podstawy  i miary kąta
i miary kąta  .
.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

