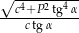/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny

Zadanie nr 8061953

Dodaj do ulubionych
Dodaj do rozwiązanych

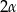Podstawą graniastosłupa prostego jest romb, którego krótsza przekątna ma długość c , a kąt ostry miarę 2α . Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi 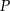P . Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.

Rozwiązanie

Zaczynamy oczywiście od szkicowego rysunku.

PIC

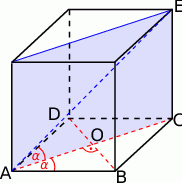
Długość przekątnej 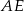AE wyliczymy z twierdzenia Pitagorasa w trójkącie prostokątnym 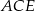ACE , najpierw jednak musimy wyliczyć długości odcinków 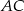AC i CE .

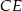Ponieważ przekątne rombu są dwusiecznymi jego kątów wewnętrznych oraz przecinają się pod kątem prostym, trójkąt 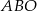ABO jest trójkątem prostokątnym o kącie ostrym α . Zatem

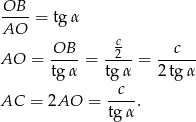
OB--= tg α AO OB c2 c AO = tg-α = tgα-= 2-tg-α- AC = 2AO = --c-. tg α

Wykorzystajmy teraz informację o podanym polu przekroju.

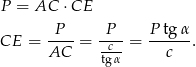
P = AC ⋅CE P P P tgα CE = ----= -c--= ------. AC tgα c

Pozostało policzyć długość przekątnej 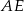AE .

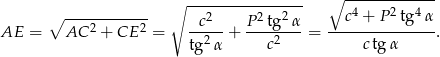
∘ ---------------- ∘ ------------- ∘ ------------ c2 P2tg2 α c4 + P2 tg 4α AE = AC 2 + CE 2 = -----+ --------= --------------. tg 2α c2 c tgα

 
Odpowiedź: √c-4+P2-tg4α ----ctg-α---

Wersja PDF