/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 23 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Różnica 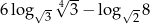 jest równa
jest równa
A) 0 B) 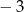 C)
C) 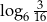 D) 3
D) 3
Dla 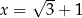 oraz
oraz 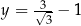 wartość wyrażenia
wartość wyrażenia 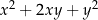 jest równa
jest równa
A) 3 B) 12 C) 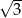 D)
D) 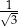
Liczba 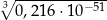 jest równa
jest równa
A) 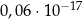 B)
B) 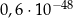 C)
C) 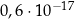 D)
D) 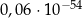
Kacper jest o 12,5% wyższy od Ali i jest wyższy od Ewy o 11 cm. Ala jest niższa od Ewy o 5%. Wzrost Kacpra jest równy
A) 171 cm B) 160 cm C) 180 cm D) 164 cm
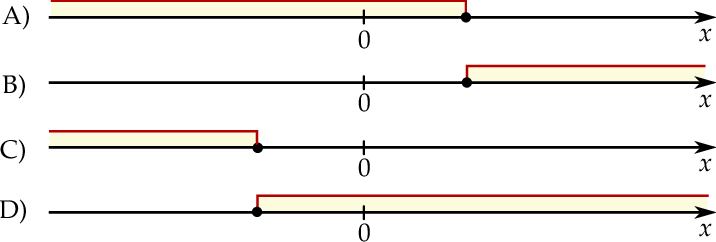
Wskaż rysunek, na którym może być przedstawiony zbiór wszystkich rozwiązań nierówności 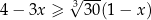 .
.
Jednym z rozwiązań równania 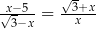 jest
jest
A) 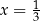 B)
B) 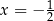 C)
C) 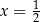 D)
D) 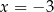
Jeśli funkcja kwadratowa 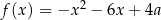 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 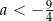 B)
B) 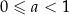 C)
C) 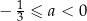 D)
D) 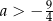
Funkcja liniowa 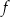 określona jest wzorem
określona jest wzorem 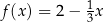 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 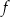 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 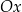 w punkcie
w punkcie 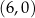
B) Funkcja 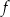 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 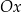 w punkcie
w punkcie 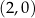
C) Funkcja 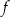 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 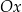 w punkcie
w punkcie 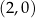
D) Funkcja 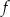 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 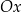 w punkcie
w punkcie 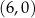
Dane są funkcje 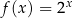 oraz
oraz 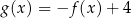 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 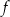 i
i 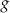
A) nie istnieje B) ma współrzędne 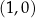
C) ma współrzędne 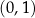 D) ma współrzędne
D) ma współrzędne 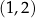
Najmniejszą wartością funkcji 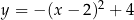 w przedziale
w przedziale 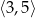 jest
jest
A) 4 B) 3 C) 0 D) 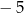
Funkcje kwadratowe 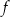 i
i 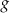 określone są wzorami
określone są wzorami 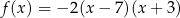 i
i 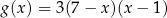 . Liczby
. Liczby 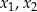 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 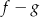 . Zatem
. Zatem
A) 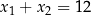 B)
B) 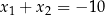 C)
C) 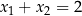 D)
D) 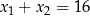
W ciągu arytmetycznym 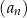 , określonym dla
, określonym dla 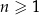 , spełniony jest warunek
, spełniony jest warunek 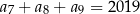 . Suma
. Suma 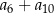 jest równa
jest równa
A) 673 B) 1346 C) 1009,5 D) 2019
Pięć liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 59049. Trzeci wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Układ równań 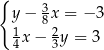
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Kąt  jest ostry i
jest ostry i 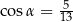 . Wtedy
. Wtedy
A) 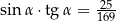 B)
B) 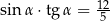 C)
C) 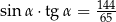 D)
D) 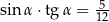
Dany jest okrąg o środku 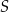 . Punkty
. Punkty 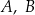 i
i 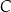 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 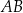 tego okręgu są oparte kąty
tego okręgu są oparte kąty 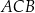 i
i 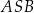 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 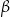 spełniają warunek
spełniają warunek 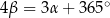 . Wynika stąd, że
. Wynika stąd, że
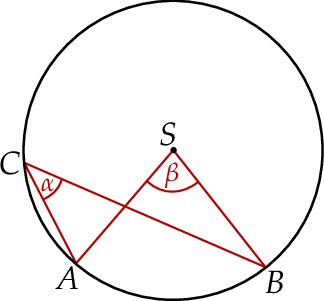
A) 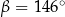 B)
B) 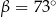 C)
C) 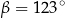 D)
D) 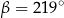
Okrąg o środku 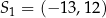 oraz okrąg o środku
oraz okrąg o środku 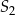 i promieniu 8 są styczne zewnętrznie w punkcie
i promieniu 8 są styczne zewnętrznie w punkcie 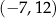 . Wtedy
. Wtedy
A) 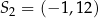 B)
B) 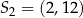 C)
C) 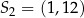 D)
D) 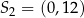
Długości boków trapezu równoramiennego są równe 19, 17, 3, 17.

Wysokość 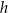 tego trapezu jest równa
tego trapezu jest równa
A) 16 B) 15 C) 14 D) 13
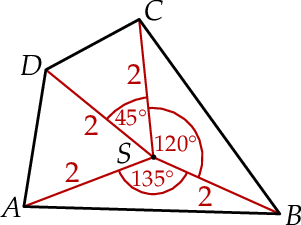
Na czworokącie 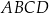 opisano okrąg o środku
opisano okrąg o środku 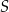 i promieniu
i promieniu 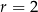 (zobacz rysunek). Pole tego czworokąta jest równe
(zobacz rysunek). Pole tego czworokąta jest równe
A) 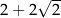 B) 4 C)
B) 4 C) 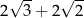 D)
D) 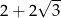
Podstawą ostrosłupa jest kwadrat 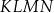 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 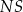 , a jej długość jest równa 6 (zobacz rysunek).
, a jej długość jest równa 6 (zobacz rysunek).

Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 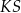 i
i 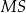 , spełnia warunek
, spełnia warunek
A) 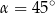 B)
B) 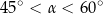 C)
C) 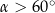 D)
D) 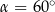
Pięć identycznych metalowych stożków o promieniu podstawy  przetopiono na jeden walec, którego wysokość jest równa
przetopiono na jeden walec, którego wysokość jest równa 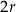 i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu
i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu  , to ile takich kul by otrzymano?
, to ile takich kul by otrzymano?
A) 32 B) 16 C) 8 D) 24
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 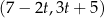 , gdzie
, gdzie 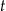 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 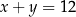 B)
B) 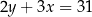 C)
C) 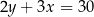 D)
D) 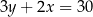
Wykonano pomiary wagi pięciu arbuzów i każde dwa rezultaty były różne. Agata zapisała wyniki w kilogramach i odchylenie standardowe jej danych było równe 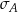 . Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe
. Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe 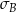 . Wynika stąd, że
. Wynika stąd, że
A) 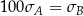 B)
B) 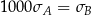 C)
C) 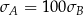 D)
D) 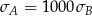
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 12 i niepodzielnych przez 8?
A) 20 B) 38 C) 75 D) 35
W tabeli poniżej przedstawione są wyniki pracy klasowej w dwóch klasach pierwszych.
| Ocena | 3,25 | 2,75 | 4,25 | 4 | 2 | 5,25 | 3,75 | 4,75 | 1 | 3 | 5 | 2,25 | 6 | 5,75 |
| Liczba ocen | 2 | 5 | 2 | 1 | 5 | 1 | 3 | 2 | 1 | 4 | 3 | 1 | 2 | 3 |
Mediana ocen w tych dwóch klasach jest równa
A) 4 B) 3 C) 3,25 D) 3,75
Zadania otwarte
Rozwiąż nierówność 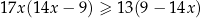 .
.
Rozwiąż równanie 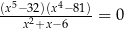 .
.
Udowodnij, że dla dowolnych liczb ujemnych 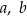 prawdziwa jest nierówność
prawdziwa jest nierówność
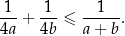
Jedenasty wyraz ciągu arytmetycznego 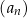 , określonego dla
, określonego dla 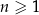 , jest równy
, jest równy 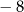 , a suma jego dziesięciu początkowych wyrazów jest równa
, a suma jego dziesięciu początkowych wyrazów jest równa 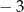 . Oblicz pierwszy wyraz i różnicę tego ciągu.
. Oblicz pierwszy wyraz i różnicę tego ciągu.
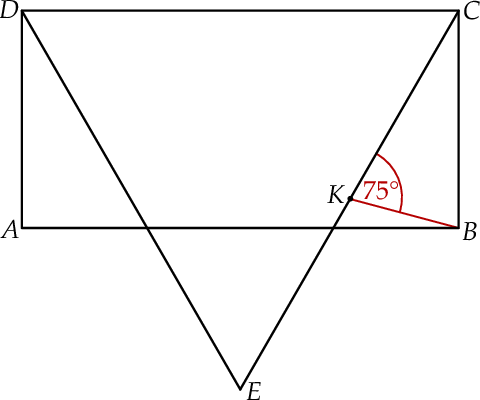
Dany jest prostokąt 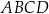 , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku
, którego jeden bok jest dwa razy dłuższy od drugiego. Na boku 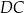 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 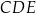 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 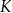 jest takim punktem odcinka
jest takim punktem odcinka 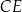 , że
, że 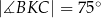 . Udowodnij, że punkt
. Udowodnij, że punkt 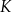 jest środkiem odcinka
jest środkiem odcinka 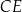 .
.
Rzucamy dziesięć razy sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych dziesięciu rzutach otrzymaliśmy dokładnie cztery razy sześć oczek, przy czym wyrzucono je w następującej konfiguracji
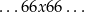
tzn. w pewnym momencie w dwóch kolejnych rzutach otrzymaliśmy szóstki, potem wyrzuciliśmy inną liczbę  oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.
oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.
W układzie współrzędnych punkty 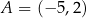 i
i 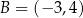 są końcami cięciwy okręgu
są końcami cięciwy okręgu  . Średnica
. Średnica 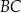 tego okręgu jest zwarta w prostej o równaniu
tego okręgu jest zwarta w prostej o równaniu 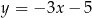 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 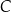 .
.
Dany jest ostrosłup prawidłowy czworokątny o wysokości 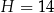 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy 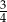 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Krótsza podstawa trapezu ma długość 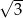 , a ramiona długości
, a ramiona długości 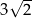 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 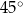 i
i 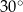 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.

