/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 4 kwietnia 2009 Czas pracy: 120 minut

Zadanie 1
(5 pkt)

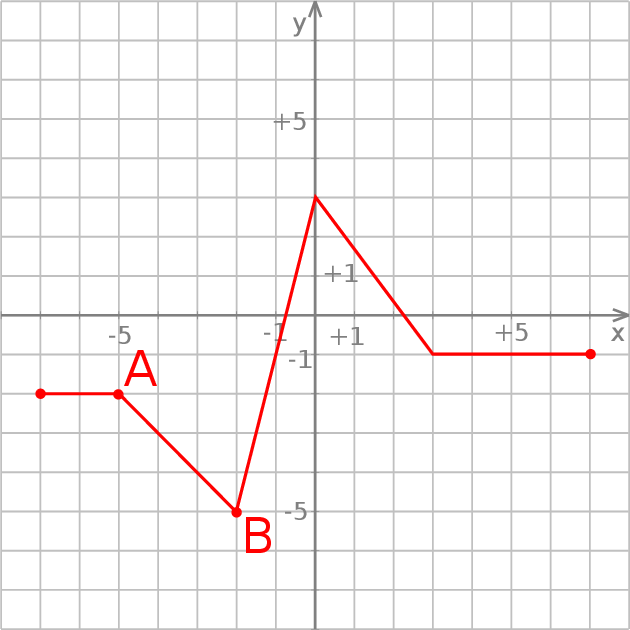
Na poniższym rysunku przedstawiono wykres funkcji 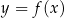y = f(x) .

ZINFO-FIGURE

  • Wyznacz zbiór wartości funkcji f .

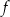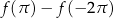  • Oblicz f(π )− f(− 2π ) .

  • Rozwiąż równanie f (x) = − 1 .

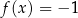  • Napisz równanie prostej AB .

Zadanie 2
(4 pkt)

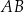Klasy IIIa i IIIb liczą odpowiednio 10 dziewcząt i 18 chłopców oraz 16 dziewcząt i 12 chłopców. Wybieramy losowo jedną z tych dwóch klas i losujemy z niej jednego ucznia. Jakie jest prawdopodobieństwo wylosowania dziewczynki?

Zadanie 3
(4 pkt)

W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.

Zadanie 4
(4 pkt)

Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?

Zadanie 5
(5 pkt)

Dzienny dochód hurtowni akumulatorów wyraża się wzorem 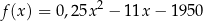f(x ) = 0,25x2 − 11x − 1950 , gdzie x oznacza liczbę sprzedanych akumulatorów.

  • Oblicz przy jakiej liczbie sprzedanych akumulatorów firma poniesie największą stratę. Oblicz wartość tej straty.

  • Oblicz ile akumulatorów należy sprzedać, aby dzienny dochód wynosił 4985.

Zadanie 6
(5 pkt)

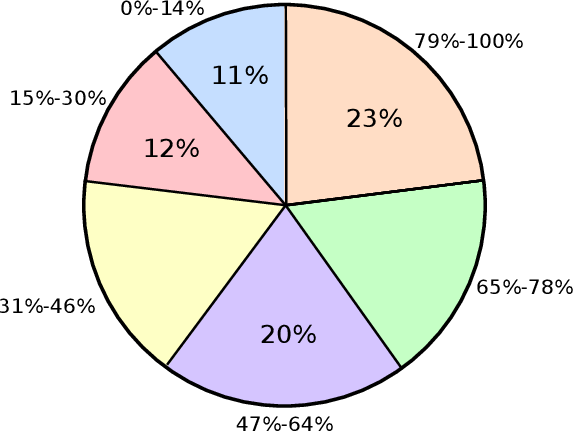
Na poniższym diagramie przedstawiono zbiorcze wyniki z egzaminu maturalnego z matematyki na poziomie rozszerzonym w 2008 roku. Diagram przedstawia rozkład wyników pogrupowanych w zależności od procentowego wyniku egzaminu.

ZINFO-FIGURE

  • Wiedząc, że egzamin na poziomie rozszerzonym zdawało 40598 maturzystów oblicz, ilu maturzystów uzyskało wynik w przedziale 0%–30%.

  • Wiedząc, że 60% maturzystów uzyskało z egzaminu co najmniej 47% punktów oblicz, jaki procent maturzystów uzyskał wynik w przedziale 31%–46%.

  • Oblicz jakie jest prawdopodobieństwo, że losowo wybrany maturzysta uzyskał wynik poniżej 47%.

Zadanie 7
(3 pkt)

O ile procent należy wydłużyć krawędź sześcianu, aby jego pole powierzchni wzrosło o 21%?

Zadanie 8
(4 pkt)

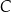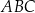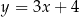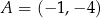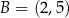Wierzchołek C trójkąta ABC leży na prostej y = 3x + 4 , a pozostałe wierzchołki mają współrzędne A = (− 1,− 4) i B = (2,5) . Uzasadnij, że pole trójkąta 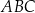ABC nie zależy od wyboru punktu 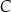C i oblicz to pole.

Zadanie 9
(3 pkt)

Ołowianą kulę o średnicy 60 cm przetopiono na walce o wysokości i promieniu podstawy równych 2 cm. Ile takich walców otrzymano?

Zadanie 10
(5 pkt)

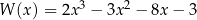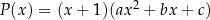Dane są wielomiany W (x) = 2x3 − 3x2 − 8x − 3 i P(x) = (x + 1 )(ax2 + bx + c) .

  • Wyznacz współczynniki 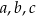a,b,c tak, aby W (x) = P (x) .

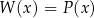  • Przedstaw wielomian 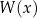W (x) jako iloczyn wielomianów liniowych.

Zadanie 11
(4 pkt)

W rosnącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40. Wyznacz pierwszy wyraz tego ciągu.

Zadanie 12
(4 pkt)

Uzasadnij, że liczba 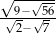√ --√--- -√-9−-√56 2− 7 jest liczbą całkowitą.

Arkusz Wersja PDF
Rozwiązania