/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 15 marca 2014 Czas pracy: 180 minut
Rozwiąż nierówność 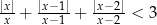 .
.
Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 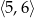 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 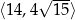 .
.
Wyznacz dziedzinę funkcji  .
.
W trójkącie 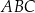 środkowa
środkowa 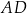 jest prostopadła do boku
jest prostopadła do boku 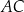 . Kąt
. Kąt 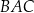 ma miarę
ma miarę 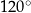 oraz
oraz 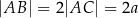 . Oblicz długość odcinka
. Oblicz długość odcinka 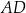 .
.
Reszta z dzielenia wielomianu 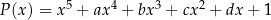 przez dwumian
przez dwumian 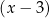 jest równa 1. Wykaż, że jeżeli liczby
jest równa 1. Wykaż, że jeżeli liczby 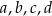 są liczbami całkowitymi to wielomian
są liczbami całkowitymi to wielomian 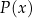 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 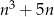 jest podzielna przez 6.
jest podzielna przez 6.
Wyznacz wszystkie wartości parametru 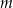 , dla których dwa różne pierwiastki rzeczywiste
, dla których dwa różne pierwiastki rzeczywiste 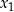 i
i 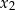 równania
równania 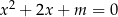 spełniają nierówność
spełniają nierówność 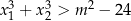 .
.
Ciągi 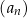 i
i 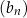 , gdzie
, gdzie 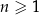 są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg
są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg 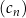 zdefiniowany wzorem
zdefiniowany wzorem 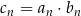 (
(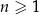 ) jest ciągiem arytmetycznym, to różnica jednego z ciągów
) jest ciągiem arytmetycznym, to różnica jednego z ciągów 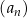 lub
lub 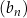 jest równa zeru.
jest równa zeru.
Rozwiąż równanie 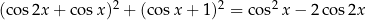 w przedziale
w przedziale 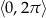 .
.
Ile jest liczb naturalnych pięciocyfrowych, których zapis dziesiętny składa się z trzech różnych cyfr?
Trójkąt o wierzchołkach 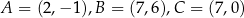 przekształcono w jednokładności o skali
przekształcono w jednokładności o skali 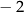 i otrzymano trójkąt o wierzchołkach
i otrzymano trójkąt o wierzchołkach 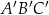 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 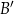 i
i 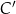 jeżeli
jeżeli 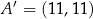 .
.
Trzy parami styczne kule o promieniach równych  znajdują się w walcu w ten sposób, że każda z kul jest styczna do obu podstaw walca, oraz do jego powierzchni bocznej. Oblicz objętość walca.
znajdują się w walcu w ten sposób, że każda z kul jest styczna do obu podstaw walca, oraz do jego powierzchni bocznej. Oblicz objętość walca.

