/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 1 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Wskaż rysunek, na którym przedstawiony jest zbiór rozwiązań nierówności 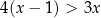 .
.

Ćwierć liczby  zwiększono o 40%. Otrzymano
zwiększono o 40%. Otrzymano
A) 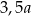 B)
B) 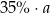 C)
C) 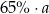 D)
D) 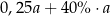
Wskaż zbiór rozwiązań nierówności 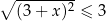 .
.
A) 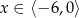 B)
B) 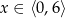 C)
C) 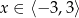 D)
D) 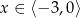
Jeśli 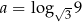 i
i 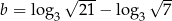 to:
to:
A) 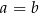 B)
B) 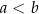 C)
C) 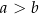 D)
D) 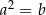
Liczbą, która nie należy do zbioru wartości funkcji 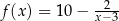 jest
jest
A) 10 B) 3 C) 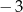 D) 0
D) 0
Punkt 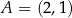 leży na wykresie funkcji liniowej
leży na wykresie funkcji liniowej 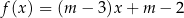 . Stąd wynika, że
. Stąd wynika, że
A) 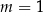 B)
B) 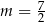 C)
C) 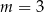 D)
D) 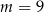
Liczba 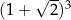 jest równa
jest równa
A) 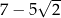 B)
B) 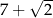 C)
C) 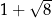 D)
D) 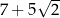
Każdy bok trójkąta prostokątnego o bokach 3, 4, 5 kolorujemy jednym z 6 kolorów tak, aby żadne dwa boki nie były pokolorowane tym samym kolorem. Ile jest takich pokolorowań?
A) 15 B) 120 C) 216 D) 20
Wierzchołek paraboli 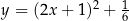 leży na prostej o równaniu
leży na prostej o równaniu
A) 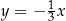 B)
B) 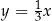 C)
C) 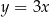 D)
D) 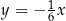
Korzystając z danego wykresu funkcji 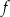 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
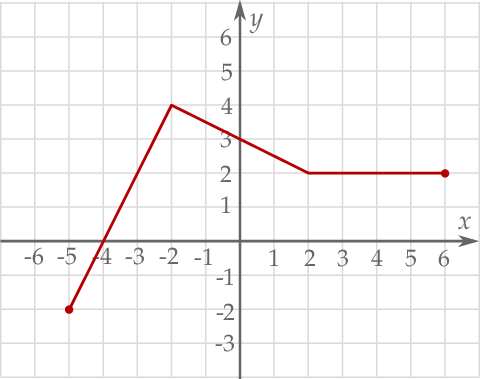
A) 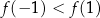 B)
B) 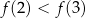 C)
C) 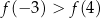 D)
D) 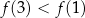
Prosta o równaniu 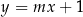 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 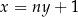 . Stąd wynika, że
. Stąd wynika, że
A) 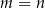 B)
B) 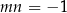 C)
C) 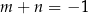 D)
D) 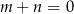
Dane są wielomiany: 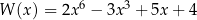 i
i 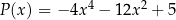 . Stopień wielomianu
. Stopień wielomianu 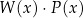 jest równy:
jest równy:
A) 24 B) 10 C) 9 D) 6
Liczby 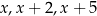 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 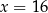 B)
B) 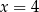 C)
C) 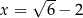 D)
D) 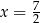
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
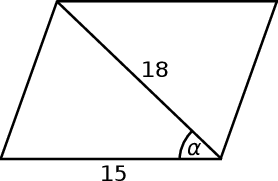
Wtedy
A) 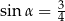 B)
B) 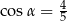 C)
C) 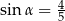 D)
D) 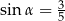
Kąt  jest ostry i
jest ostry i 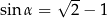 . Wartość wyrażenia
. Wartość wyrażenia 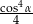 jest równa
jest równa
A) 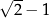 B)
B) 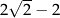 C)
C) 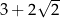 D)
D) 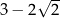
Średnice 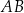 i
i 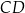 okręgu o środku
okręgu o środku 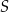 przecinają się pod kątem
przecinają się pod kątem 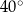 (tak jak na rysunku).
(tak jak na rysunku).
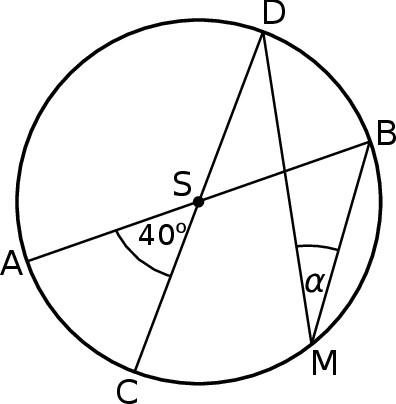
Miara kąta  jest równa
jest równa
A) 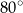 B)
B) 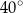 C)
C) 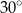 D)
D) 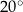
Krótsza przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła wpisanego w ten sześciokąt jest równe
A) 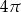 B)
B) 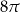 C)
C) 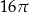 D)
D) 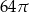
Równanie okręgu wpisanego w romb o wierzchołkach 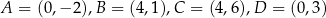 ma postać
ma postać
A) 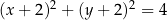 B)
B) 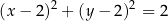
C) 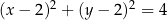 D)
D) 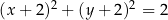
Na rysunku przedstawiono wykres funkcji 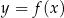 .
.
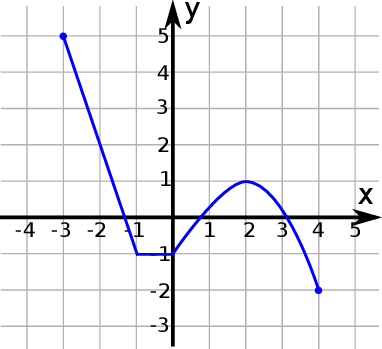
W którym z przedziałów, funkcja przyjmuje wartość 1?
A) 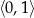 B)
B) 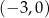 C)
C) 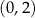 D)
D) 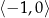
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Liczby 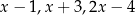 w podanej kolejności tworzą ciąg arytmetyczny. Wtedy
w podanej kolejności tworzą ciąg arytmetyczny. Wtedy  jest równe
jest równe
A) 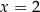 B)
B) 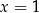 C)
C) 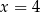 D)
D) 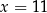
Jaką liczbę można wstawić pomiędzy 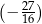 i
i  , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A)  B)
B) 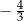 C)
C)  D)
D) 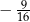
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
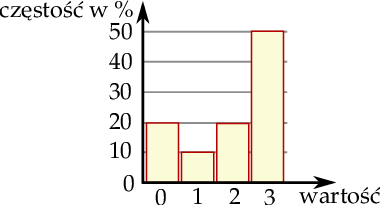
A) 2 B) 1 C) 1,5 D) 1,8
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 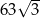 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 4 B) 3 C) 6 D) 36
Zadania otwarte
Rozwiąż równanie 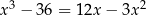 .
.
Rozwiąż nierówność 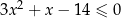 .
.
Kąt  jest ostry i
jest ostry i 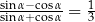 . Oblicz
. Oblicz 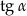 .
.
W 8 pudełkach umieszczamy 5 ponumerowanych kulek tak, aby w żadnym pudełku nie było więcej niż jednej kulki. Na ile sposobów możemy to zrobić?
Wyznacz współrzędne punktu 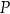 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 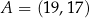 i
i 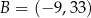 w stosunku
w stosunku 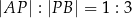 .
.
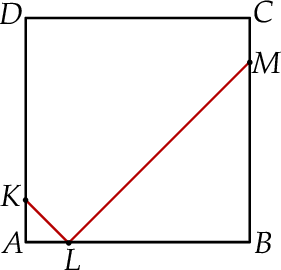
Na bokach 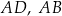 i
i 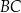 kwadratu
kwadratu 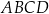 wybrano punkty
wybrano punkty 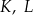 i
i 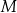 w ten sposób, że
w ten sposób, że 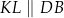 i
i 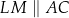 . Uzasadnij, że
. Uzasadnij, że 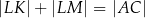 .
.
Ciąg 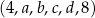 jest geometryczny. Oblicz
jest geometryczny. Oblicz 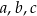 i
i 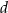 .
.
Pociąg towarowy pokonał trasę długości 208 km. Gdyby średnia prędkość pociągu była większa o 13 km/h to tę samą trasę pociąg pokonałby w czasie o 48 minut krótszym. Oblicz średnią prędkość z jaką pociąg pokonał tę trasę.
Objętość ostrosłupa prawidłowego czworokątnego 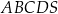 o podstawie
o podstawie 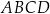 jest równa 224, a promień okręgu opisanego na podstawie
jest równa 224, a promień okręgu opisanego na podstawie 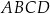 jest równy
jest równy 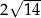 . Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
. Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.

