/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony 14 stycznia 2014 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.

Zadanie 2
(4 pkt)

Rozwiąż równanie 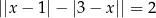||x− 1|− |3 − x|| = 2 .

Zadanie 3
(4 pkt)

Jednym z pierwiastków wielomianu 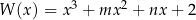W (x) = x3 + mx 2 + nx + 2 jest liczba 1. Reszta z dzielenia wielomianu 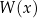W (x) przez dwumian 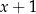x+ 1 jest równa 4. Oblicz współczynniki 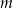m i n .

Zadanie 4
(4 pkt)

Dany jest okrąg o równaniu 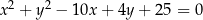x2 + y2 − 10x + 4y + 25 = 0 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.

Zadanie 5
(4 pkt)

Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.

Zadanie 6
(4 pkt)

Rozwiąż równanie 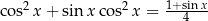2 2 1+ sinx cos x + sin xco s x = ---4-- w przedziale ⟨0,2π ⟩ .

Zadanie 7
(5 pkt)

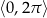Ciąg liczbowy 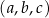(a,b,c) jest arytmetyczny i 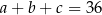a+ b+ c = 36 , natomiast ciąg 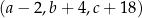(a− 2,b+ 4,c+ 1 8) jest geometryczny. Oblicz a,b,c .

Zadanie 8
(5 pkt)

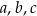Suma długości dwóch sąsiednich boków w pewnym trójkącie jest równa 14, a kąt między tymi bokami ma miarę 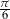π6- . Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.

Zadanie 9
(6 pkt)

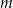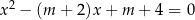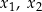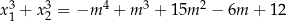Oblicz wszystkie wartości parametru m , dla których równanie x2 − (m + 2)x + m + 4 = 0 ma dwa różne pierwiastki rzeczywiste x1, x 2 takie, że x3 + x3 = −m 4 + m 3 + 15m 2 − 6m + 12 1 2 .

Zadanie 10
(4 pkt)

W graniastosłupie prawidłowym czworokątnym przekątne ścian bocznych, wychodzące z tego samego wierzchołka, mają długość 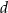d i tworzą kąt o mierze α . Oblicz objętość tego graniastosłupa.

Zadanie 11
(5 pkt)

Liczba uczniów w klasie jest 812 razy mniejsza od liczby utworzonych z nich uporządkowanych trójek. Oblicz prawdopodobieństwo wylosowania trzech osób, które (w kolejności losowania) są zapisane w dzienniku pod numerami pierwszym, drugim, i trzecim.

Arkusz Wersja PDF
Rozwiązania