/Szkoła średnia/Zadania maturalne

Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony (technikum) 2 czerwca 2015 Czas pracy: 180 minut

Zadanie 1
(6 pkt)

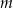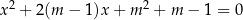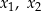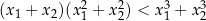Wyznacz wszystkie wartości parametru m , dla których równanie x2 + 2(m − 1 )x+ m2 + m − 1 = 0 ma dwa różne pierwiastki rzeczywiste x1, x2 takie, że 2 2 3 3 (x 1 + x 2)(x1 + x2) < x1 + x2 .

Zadanie 2
(4 pkt)

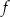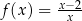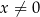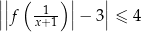Funkcja f jest określona wzorem x−2- f(x ) = x dla wszystkich liczb rzeczywistych x takich, że x ⁄= 0 . Rozwiąż nierówność || ( )| | ||||f -1--|| − 3|| ≤ 4 x+1 .

Zadanie 3
(4 pkt)

Rozwiąż równanie 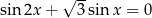-- sin 2x + √ 3 sin x = 0 w przedziale ⟨0,2π ⟩ .

Zadanie 4
(3 pkt)

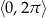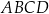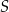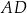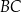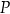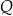W trapez ABCD wpisano okrąg o środku S . Okrąg ten jest styczny do ramion AD i BC tego trapezu w punktach odpowiednio P i Q (zobacz rysunek).

ZINFO-FIGURE

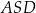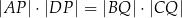Uzasadnij, że trójkąt ASD jest prostokątny. Wykaż, że |AP |⋅|DP | = |BQ | ⋅|CQ | .

Zadanie 5
(3 pkt)

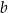Wykaż, że dla każdej dodatniej i różnej od jedności liczby a i dla każdej dodatniej i różnej od jedności liczby b spełniona jest równość

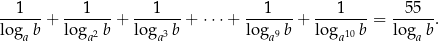
1 1 1 1 1 55 ------+ -------+ -------+ ⋅⋅⋅+ -------+ --------= ------. lo gab lo ga2 b loga3 b lo ga9 b loga10 b logab

Zadanie 6
(5 pkt)

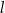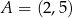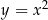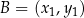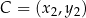Prosta l , na której leży punkt A = (2,5) , przecina parabolę o równaniu y = x2 w dwóch różnych punktach B = (x1,y1) i C = (x2,y2) . Oblicz wartość współczynnika kierunkowego prostej 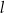l , przy której suma 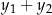y + y 1 2 osiągnie wartość najmniejszą.

Zadanie 7
(6 pkt)

Trzy liczby, których suma jest równa 105, są kolejnymi wyrazami rosnącego ciągu geometrycznego. Pierwsza z tych liczb jest jednocześnie pierwszym, druga szóstym, a trzecia dwudziestym szóstym wyrazem pewnego ciągu arytmetycznego. Oblicz te liczby.

Zadanie 8
(6 pkt)

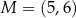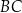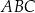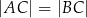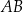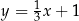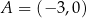Punkt M = (5,6) jest środkiem ramienia BC trójkąta równoramiennego ABC , w którym |AC | = |BC | . Podstawa AB tego trójkąta jest zawarta w prostej o równaniu 1 y = 3x + 1 oraz A = (− 3,0) . Oblicz współrzędne wierzchołka 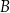B tego trójkąta.

Zadanie 9
(5 pkt)

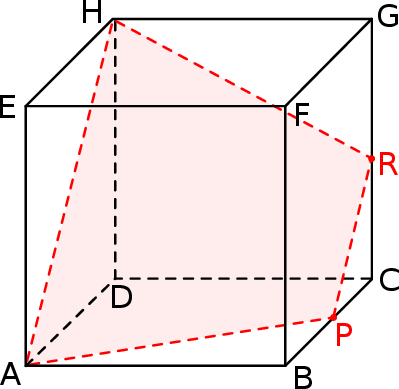
Dany jest sześcian 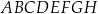ABCDEF GH o krawędzi długości 2. Punkt 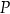P jest środkiem krawędzi 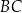BC . Płaszczyzna 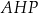AHP przecina krawędź 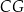CG w punkcie 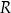R (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty 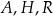A ,H ,R i P .

ZINFO-FIGURE

Zadanie 10
(4 pkt)

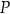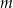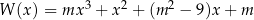Wyznacz wszystkie wartości parametru m , dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu W (x) = mx 3 + x2 + (m 2 − 9)x+ m .

Zadanie 11
(4 pkt)

Każda z urn oznaczonych liczbami 1, 2, 3 zawiera po 3 kule czarne i 4 białe, a każda urna oznaczona liczbami 4, 5, 6 zawiera po 3 czarne i 2 białe kule. Rzucamy sześcienną kostką do gry, a następnie z urny o numerze równym liczbie wyrzuconych oczek losujemy bez zwracania 2 kule. Co jest bardziej prawdopodobne: wylosowanie dwóch kul czarnych, czy dwóch kul białych?

Arkusz Wersja PDF
Rozwiązania