/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 29 marca 2014 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

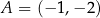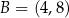Dane są punkty A = (− 1,− 2) i B = (4,8) . Wyznacz te punkty prostej 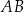AB , dla których różnica odległości od punktu 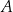A i odległości od punktu 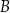B jest większa niż odległość od punktu (0,0) .

Zadanie 2
(5 pkt)

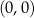Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 28 oraz suma ich odwrotności jest równa 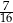716- .

Zadanie 3
(4 pkt)

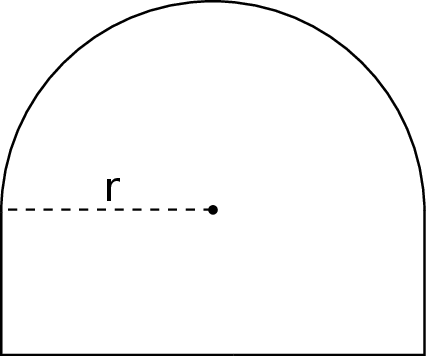
Przedstawiona na rysunku figura składa się z półkola i prostokąta. Oblicz maksymalne pole tej figury, jeżeli jej obwód jest równy 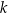k .

ZINFO-FIGURE

Zadanie 4
(4 pkt)

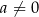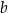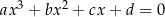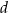Dane są liczby wymierne a ⁄= 0 i b takie, że równanie 3 2 ax + bx + cx + d = 0 ma dwa pierwiastki wymierne. Wykaż, że c i d są liczbami wymiernymi.

Zadanie 5
(4 pkt)

Rozwiąż równanie cos22x + 4 cos2x − 2 = 0 w zbiorze ⟨0,2π ⟩ .

Zadanie 6
(5 pkt)

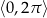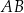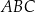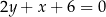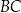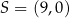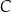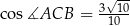Przyprostokątna AB trójkąta prostokątnego ABC jest zawarta w prostej o równaniu 2y + x + 6 = 0 , a środek jego przeciwprostokątnej BC ma współrzędne S = (9,0) . Oblicz współrzędne wierzchołka C jeżeli √-- 3-10- co s∡ACB = 10 .

Zadanie 7
(4 pkt)

Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości a . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż 1 a 4 .

Zadanie 8
(4 pkt)

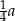Rozwiąż równanie 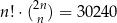n !⋅(2n) = 30240 n .

Zadanie 9
(4 pkt)

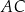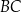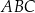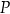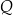Na ramionach AC i BC trójkąta równoramiennego ABC wybrano punkty P i Q w ten sposób, że odcinek 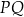PQ jest równoległy do podstawy 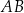AB i styczny do okręgu wpisanego w trójkąt 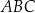ABC . Wykaż, że pole trójkąta 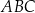ABC jest równe

2∘ ------------ |AB-|---|AB-|⋅|P-Q-|. 2(|AB |− |P Q |)

Zadanie 10
(6 pkt)

Podstawą ostrosłupa o objętości 30 jest trójkąt równoramienny o ramieniu długości 5 i podstawie długości 6. Oblicz pole powierzchni bocznej ostrosłupa wiedząc, że wszystkie krawędzie boczne mają jednakową długość.

Zadanie 11
(5 pkt)

Każdą krawędź sześcianu kolorujemy jednym z 6 kolorów, wśród których są kolory: biały i czarny. Oblicz prawdopodobieństwo, że wśród pokolorowanych krawędzi są dokładnie 3 krawędzie białe i 2 czarne. Wynik podaj w postaci ułamka nieskracalnego.

Arkusz Wersja PDF
Rozwiązania