/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom rozszerzony 25 sierpnia 2009 Czas pracy: 180 minut
Dla jakich 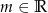 równanie
równanie 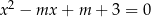 ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?
Wyznacz taki punkt 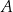 na prostej
na prostej 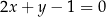 , by suma kwadratów jego odległości od osi układu była najmniejsza.
, by suma kwadratów jego odległości od osi układu była najmniejsza.
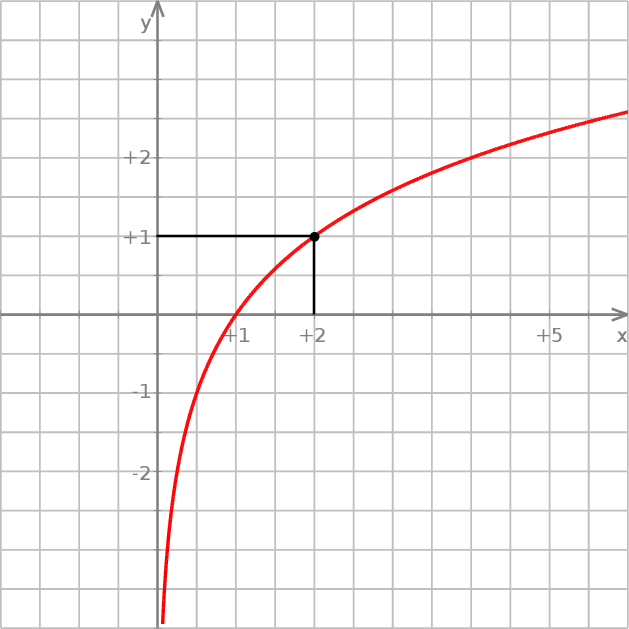
Dany jest wykres funkcji logarytmicznej 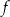 .
.
-
Wyznacz wzór funkcji
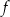 .
. -
Narysuj wykres funkcji
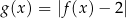 .
. -
Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
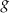 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 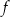 .
.
Wykaż, że jeśli 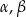 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 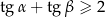 .
.
Rozwiąż w zbiorze 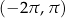 równanie
równanie 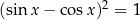 .
.
Ciąg 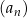 jest arytmetyczny oraz
jest arytmetyczny oraz 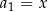 i
i 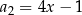 . Wiedząc, że
. Wiedząc, że 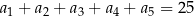 oblicz
oblicz  oraz sumę
oraz sumę 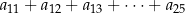 .
.
Trapez równoramienny 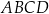 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Przekątna trapezu tworzy z dłuższą podstawą kąt
. Przekątna trapezu tworzy z dłuższą podstawą kąt  . Wyznacz obwód tego trapezu.
. Wyznacz obwód tego trapezu.
Na przyprostokątnych 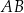 i
i 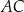 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 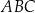 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 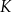 i
i 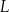 tak, że
tak, że 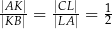 . Odcinki
. Odcinki 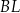 i
i 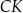 przecinają się w punkcie
przecinają się w punkcie 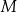 . Oblicz
. Oblicz 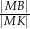 .
.
Ile punktów wspólnych ma prosta 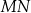 z okręgiem
z okręgiem 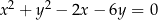 jeśli
jeśli 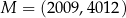 oraz
oraz 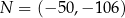 .
.
Dane są punkty 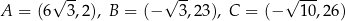 . Opisz za pomocą nierówności półpłaszczyznę o krawędzi
. Opisz za pomocą nierówności półpłaszczyznę o krawędzi 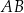 , do której należy punkt
, do której należy punkt 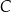 .
.
Podstawą ostrosłupa 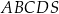 jest prostokąt
jest prostokąt 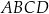 o bokach długości
o bokach długości 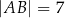 i
i 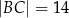 . Krawędź
. Krawędź 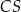 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 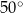 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Do kina wybrało się 7 osób, wśród nich Basia i Janek. Wszyscy usiedli w jednym rzędzie, w którym jest dokładnie 7 wolnych miejsc. Oblicz, na ile sposobów wymienione osoby mogą zająć miejsca tak, by Basia i Janek siedzieli obok siebie. Oblicz też prawdopodobieństwo tego, że przy losowym zajmowaniu miejsc Basia i Janek nie siedzą obok siebie.

