/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 2 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Dane są liczby 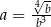 ,
, 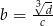 ,
, 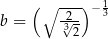 ,
, 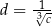 . Zatem
. Zatem
A) 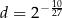 B)
B) 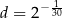 C)
C) 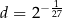 D)
D) 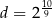
Okrąg o równaniu 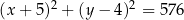 jest styczny do okręgu o środku
jest styczny do okręgu o środku 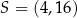 i promieniu
i promieniu  . Wynika stąd, że
. Wynika stąd, że
A) 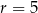 B)
B) 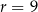 C)
C) 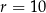 D)
D) 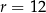
Liczba 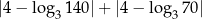 jest równa
jest równa
A) 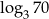 B)
B) 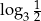 C)
C) 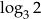 D)
D) 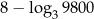
Rozwiązaniem nierówności 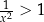 jest zbiór
jest zbiór
A) 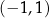 B)
B) 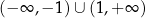 C)
C) 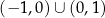 D)
D) 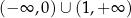
Granica 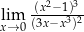
A) jest równa 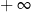 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 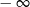
Zadania otwarte
Punkt 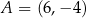 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem 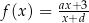 , gdy
, gdy 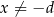 . Oblicz iloraz
. Oblicz iloraz 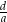 .
.
Napisz równanie stycznej do wykresu funkcji 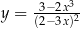 w punkcie
w punkcie 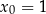 .
.
Punkty 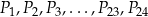 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 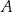 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 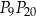 i
i 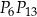 .
.
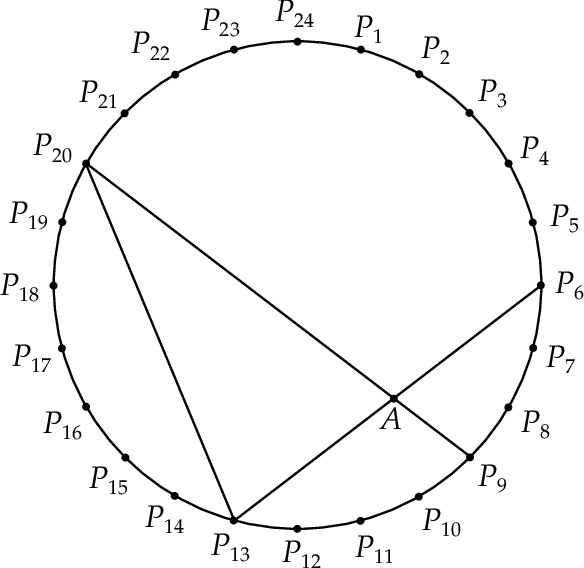
Udowodnij, że trójkąt 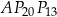 jest równoramienny.
jest równoramienny.
O zdarzeniach losowych 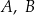 wiadomo, że:
wiadomo, że: 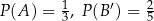 i
i 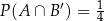 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 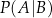 .
.
Wyznacz zbiór wartości funkcji 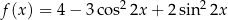 dla
dla 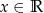 .
.
Punkty 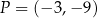 ,
, 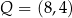 i
i 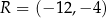 są środkami odpowiednio boków
są środkami odpowiednio boków 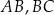 i
i 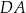 równoległoboku
równoległoboku 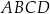 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 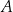 tego równoległoboku.
tego równoległoboku.
Czterdzieści osób usadzono w sposób losowy przy czterech dziesięcioosobowych okrągłych stołach. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że trzy ustalone wcześniej osoby siedzą na trzech sąsiednich miejscach.
Wyrazy ciągu geometrycznego 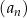 , określonego dla
, określonego dla 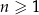 , spełniają układ równań
, spełniają układ równań
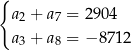
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 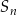 jest równa 177148.
jest równa 177148.
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
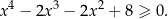
Punkt 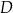 jest środkiem boku
jest środkiem boku 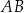 trójkąta
trójkąta 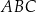 oraz
oraz 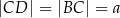 ,
, 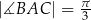 . Oblicz długości boków
. Oblicz długości boków 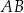 i
i 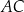 trójkąta
trójkąta 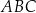 .
.
Wyznacz wszystkie wartości parametru 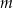 , dla których równanie
, dla których równanie
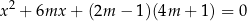
ma dwa różne rozwiązania 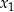 ,
, 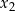 spełniające warunki:
spełniające warunki: 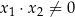 oraz
oraz 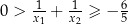 .
.
Spodek wysokości ostrosłupa 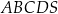 pokrywa się ze środkiem rombu
pokrywa się ze środkiem rombu 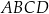 w jego podstawie oraz
w jego podstawie oraz 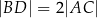 ,
, 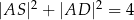 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 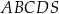 jeżeli wiadomo, że pole trójkąta
jeżeli wiadomo, że pole trójkąta 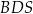 jest największe możliwe.
jest największe możliwe.

