/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 28 marca 2015 Czas pracy: 180 minut
Która z liczb jest większa: 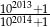 , czy
, czy 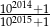 ?
?
Dany jest trapez prostokątny 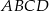 o podstawach
o podstawach 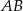 i
i 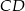 , w którym boki
, w którym boki 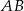 i
i 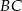 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 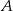 i
i 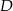 przecinają się w punkcie
przecinają się w punkcie 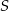 leżącym na boku
leżącym na boku 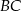 . Wykaż, że
. Wykaż, że 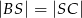 .
.
Rozwiąż nierówność 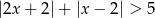 .
.
Naszkicuj wykresy funkcji 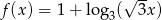 i
i 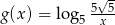 , gdzie
, gdzie 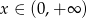 . Odczytaj z wykresów zbiór rozwiązań nierówności
. Odczytaj z wykresów zbiór rozwiązań nierówności 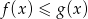 .
.
Wyznacz wszystkie liczby naturalne dodatnie 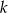 , dla których równanie
, dla których równanie 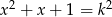 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi.
Reszta z dzielenia wielomianu 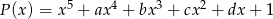 przez dwumian
przez dwumian 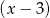 jest równa 1. Wykaż, że jeżeli liczby
jest równa 1. Wykaż, że jeżeli liczby 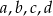 są liczbami całkowitymi to wielomian
są liczbami całkowitymi to wielomian 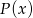 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
W trójkącie prostokątnym 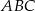 przyprostokątne mają długości
przyprostokątne mają długości 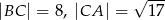 . Na boku
. Na boku 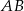 wybrano punkt
wybrano punkt 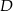 tak, że
tak, że 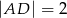 . Oblicz sinus kąta
. Oblicz sinus kąta 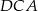 .
.
Podstawą ostrosłupa 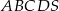 jest prostokąt
jest prostokąt 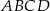 , a krawędź boczna
, a krawędź boczna 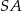 jest jego wysokością. Wykaż, że suma kwadratów pól ścian
jest jego wysokością. Wykaż, że suma kwadratów pól ścian 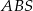 i
i 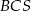 jest równa sumie kwadratów pól ścian
jest równa sumie kwadratów pól ścian 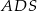 i
i 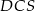 .
.
Z punktu 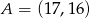 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 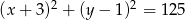 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Wykaż, że jeżeli 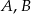 są podzbiorami
są podzbiorami 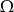 oraz
oraz 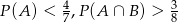 , to
, to 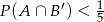 .
.
Rozwiąż równanie 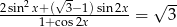 .
.
W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi  objętości stożka.
objętości stożka.

