/Szkoła średnia/Zadania maturalne
Kombinatoryka XII Polygon Matematyczny
poziom rozszerzony Styczeń 2020
Na przyjęciu spotkała się pewna liczba znajomych. Wszyscy znajomi przywitali się podaniem ręki. Nastąpiło 10 powitań. Ilu przyjaciół się spotkało?
Rozwiąż równanie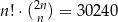 
.
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Zbiór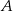 
ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór 
?
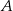Wyznacz wszystkie liczby naturalne 
spełniające równanie
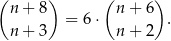
Na ile sposobów można rozmieścić sześć ponumerowanych kul w pięciu ponumerowanych szufladach tak, aby w każdej szufladzie była przynajmniej jedna kula.
Ile jest liczb naturalnych pięciocyfrowych, których zapis dziesiętny składa się z trzech różnych cyfr?
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie trzy cyfry nieparzyste.
Ile jest permutacji zbioru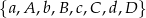 
takich, w których mała litera stoi przed dużą (niekoniecznie obok) np. 
?
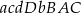Ile jest liczb naturalnych ośmiocyfrowych, których suma cyfr jest równa 4?
W pewnym budynku biurowym przydzielono pracownikom pięciocyfrowe kody bezpieczeństwa, przy czym każdy kod musiał spełniać następujące dwa warunki:
(1) kod musi zawierać co najmniej 3 różne cyfry
(2) kod musi zawierać co najmniej jedną cyfrę parzystą i co najmniej jedną cyfrę nieparzystą.
Ile jest kodów spełniających powyższe warunki?
Ile jest takich czwórek liczb całkowitych i dodatnich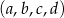 
, które spełniają równanie 
.
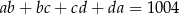